Question

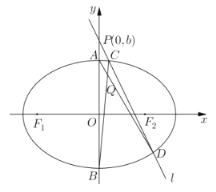
【题目】年前某市质监部门根据质量管理考核指标对本地的500家食品生产企业进行考核，然后通过随机抽样抽取其中的50家，统计其考核成绩（单位：分），并制成如下频率分布直方图.

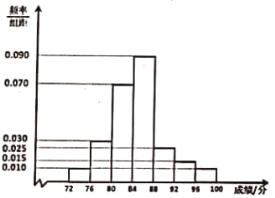
（1）求这50家食品生产企业考核成绩的平均数（同一组中的数据用该组区间的中点值为代表）及中位数a（精确到0.01）

（2）该市质监部门打算举办食品生产企业质量交流会，并从这50家食品生产企业中随机抽取4家考核成绩不低于88分的企业发言，记抽到的企业中考核成绩在的企业数为X，求X的分布列与数学期望

（3）若该市食品生产企业的考核成绩X服从正态分布其中近似为50家食品生产企业考核成绩的平均数，近似为样本方差，经计算得，利用该正态分布，估计该市500家食品生产企业质量管理考核成绩高于90.06分的有多少家?（结果保留整数）.

附参考数据与公式：

则，.

Answer 1

【答案】（1），；（2）分布列见解析，；（3）79家

【解析】

（1）利用频率分布直方图的性质能求出这50家食品生产企业考核成绩的平均数和中位数；

（2）这50家食品生产企业中考核成绩不低于88分的企业有10家，其中考核成绩在内的企业有5家，得出随机变量的可能取值，分别求出相应的概率，得出分布列，求得数学期望；

（3）根据题意得，由此能求出估计该市500家食品生产企业质量管理考核成绩高于90.06分的有多少家.

（1）由题意，这50家食品生产企业考核成绩的平均数为：

（分）,

由频率分布图可知内，所以，

解得分.

（2）根据题意，这50家食品生产企业中考核成绩不低于88分的企业有:

（家），

其中考核成绩在内的企业有（家），

所以X可能取值有0，1，2，3，4

则，，，，，

所以X的分布列为

X	0	1	2	3	4
P

所以.

（3）由题意得，所以，

所以，所以（家），

所以500家食品生产企业质量管理考核成绩高于90.06分的有79家.