题目内容

设点P在椭圆 $数学公式$ 上，点F为椭圆的右焦点，PF垂直于x轴，椭圆的右准线与x轴交于K点，则|PF|与|FK|的比值为 ________．

$\text{[math]}$
分析：过点P做右准线的垂线，垂足为E，则可推断出|FK|=|PE|，根据椭圆方程求得椭圆的离心率，然后根据椭圆的第二定义可知 $\text{[math]}$ =e，进而可求得|PF|与|FK|的比值．
解答：过点P做右准线的垂线，垂足为E，则|FK|=|PE|
椭圆的方程可知a=2，b= $\text{[math]}$ ，c= $\text{[math]}$ =1
∴e= $\text{[math]}$ = $\text{[math]}$
根据椭圆的第二定义可知 $\text{[math]}$ =e= $\text{[math]}$
∴|PF|与|FK|的比值为 $\text{[math]}$
故答案为： $\text{[math]}$
点评：本题主要考查了椭圆的简单性质．解题的关键是利用了椭圆的第二定义．

练习册系列答案

1日1练口算题卡系列答案

举一反三同步巧讲精练系列答案

口算与应用题卡系列答案

培优新题库系列答案

教材备考笔记系列答案

竖式计算卡系列答案

名师点睛字词句段篇系列答案

名校直通车系列答案

初中学业水平考查系列答案

实验活动练习册系列答案

相关题目

已知椭圆Γ的方程为

=1(a＞b＞0)，A（0，b）、B（0，-b）和Q（a，0）为Γ的三个顶点．
（1）若点M满足

)，求点M的坐标；
（2）设直线l₁：y=k₁x+p交椭圆Γ于C、D两点，交直线l₂：y=k₂x于点E．若k1•k2=-

，证明：E为CD的中点；
（3）设点P在椭圆Γ内且不在x轴上，如何构作过PQ中点F的直线l，使得l与椭圆Γ的两个交点P₁、P₂满足

？令a=10，b=5，点P的坐标是（-8，-1），若椭圆Γ上的点P₁、P₂满足

，求点P₁、P₂的坐标．

设点P在椭圆

=1上，点F为椭圆的右焦点，PF垂直于x轴，椭圆的右准线与x轴交于K点，则|PF|与|FK|的比值为

设点P在椭圆

上，点F为椭圆的右焦点，PF垂直于x轴，椭圆的右准线与x轴交于K点，则|PF|与|FK|的比值为．

设点P在椭圆

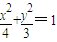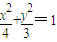上，点F为椭圆的右焦点，PF垂直于x轴，椭圆的右准线与x轴交于K点，则|PF|与|FK|的比值为．