题目内容
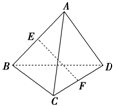
A是△BCD所在平面外一点，M、N分别是△ABC和△ACD的重心，若BD=4，试求MN的长．
分析：利用三角形的重心的性质分三角形的中线为2：1的关系，利用向量的运算法则及三角形的中位线的性质求出MN与BD的关系．
解答：解：连接AM并延长与BC相交于E，连接AN并延长与CD相交于F，则E、F分别是BC及CD的中点．
∵
=
-
=
-
=
（
-
）=
∴|
=
|
∵E、F分别是BC及CD的中点
∴|
|=
|
|
∴|
|=
|
|=
BD=
．
∵
| MN |
| AN |
| AM |
| 2 |
| 3 |
| AF |
| 2 |
| 3 |
| AE |
| 2 |
| 3 |
| AF |
| AE |
| 2 |
| 3 |
| EF |
∴|
| MN| |
| 2 |
| 3 |
| EF| |
∵E、F分别是BC及CD的中点
∴|
| EF |
| 1 |
| 2 |
| BD |
∴|
| MN |
| 1 |
| 3 |
| BD |
| 1 |
| 3 |
| 4 |
| 3 |
点评：本题考查三角形的重心性质；向量的三角形法则；及三角形的中位线性质．
练习册系列答案
暑假作业海燕出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目
如图，点A是△BCD所在平面外一点，AD=BC，E、F分别是AB、CD的中点．