题目内容
若函数f(x)在给定区间M上,存在正数t,使得对于任意x∈M,有x+t∈M,且f(x+t)≥f(x),则称f(x)为M上的t级类增函数,则以下命题正确的是( )
A.函数f(x)=
| ||||
| B.函数f(x)=|log2(x-1)|是(1,+∞)上的1级类增函数 | ||||
C.若函数f(x)=sinx+ax为[
| ||||
| D.若函数f(x)=x2-3x为[1,+∞)上的t级类增函数,则实数t的取值范围为[1,+∞) |
∵f(x)=
+x,
∴f(x+1)-f(x)=
+x+1-
-x
=
-
+1≥0在(1,+∞)上不成立,
故A不正确;
∵f(x)=|log2(x-1)|,
∴f(x+1)-f(x)=|log2x|-|log2(x-1)|≥0在(1,+∞)上不成立,
故B不正确;
∵函数f(x)=sinx+ax为[
,+∞)上的
级类增函数,
∴sin(x+
)+a(x+
)≥sinx+ax,
∴sinxcos
+cosxsin
+ax+
a≥sinx+ax,
∴
cosx+
a≥
sinx,
当x=
时,
a≥
,a≥
,
∴实数a的最小值不为2,故C不正确;
∵f(x)=x2-3x为[1,+∞)上的t级类增函数,
∴(x+t)2-3(x+t)≥x2-3x,
∴2tx+t2-3t≥0,
t≥3-2x∈[1,+∞),
故D成立.
故选D.
| 4 |
| x |
∴f(x+1)-f(x)=
| 4 |
| x+1 |
| 4 |
| x |
=
| 4 |
| x+1 |
| 4 |
| x |
故A不正确;
∵f(x)=|log2(x-1)|,
∴f(x+1)-f(x)=|log2x|-|log2(x-1)|≥0在(1,+∞)上不成立,
故B不正确;
∵函数f(x)=sinx+ax为[
| π |
| 2 |
| π |
| 3 |
∴sin(x+
| π |
| 3 |
| π |
| 3 |
∴sinxcos
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
∴
| ||
| 2 |
| π |
| 3 |
| 1 |
| 2 |
当x=
| π |
| 2 |
| π |
| 3 |
| 1 |
| 2 |
| 3 |
| 2π |
∴实数a的最小值不为2,故C不正确;
∵f(x)=x2-3x为[1,+∞)上的t级类增函数,
∴(x+t)2-3(x+t)≥x2-3x,
∴2tx+t2-3t≥0,
t≥3-2x∈[1,+∞),
故D成立.
故选D.

练习册系列答案
相关题目
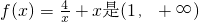 上的1级类增函数
上的1级类增函数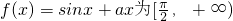 上的
上的 级类增函数,则实数a的最小值为2
级类增函数,则实数a的最小值为2 上的1级类增函数
上的1级类增函数 上的
上的 级类增函数,则实数a的最小值为2
级类增函数,则实数a的最小值为2 上的1级类增函数
上的1级类增函数 上的
上的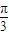 级类增函数,则实数a的最小值为2
级类增函数,则实数a的最小值为2