题目内容
已知数列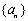 (
(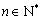 ,
,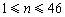 )满足
)满足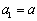 ,
, 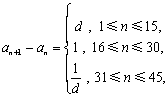 其中
其中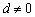 ,
,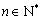 .
.
(1)当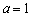 时,求
时,求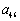 关于
关于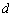 的表达式,并求
的表达式,并求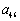 的取值范围;
的取值范围;
(2)设集合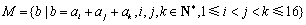 .
.
①若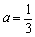 ,
,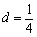 ,求证:
,求证: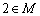 ;
;
②是否存在实数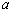 ,
,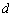 ,使
,使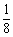 ,
,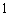 ,
,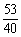 都属于
都属于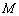 ?若存在,请求出实数
?若存在,请求出实数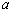 ,
,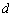 ;若不存在,请说明理由.
;若不存在,请说明理由.
解:(1)当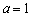 时,
时,
 ,
, ,
, .
.
因为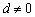 ,
, ,或
,或 ,
,
所以 .
.
(2)①由题意 ,
, ,
, .
.
令 ,得
,得 .
.
因为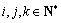 ,
, ,
,
所以令 ,则
,则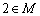 .
.
②不存在实数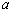 ,
,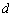 ,使
,使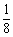 ,
,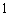 ,
,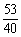 同时属于
同时属于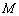 .
.
假设存在实数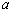 ,
,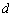 ,使
,使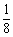 ,
,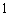 ,
,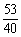 同时属于
同时属于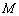 .
.
 ,∴
,∴ ,
,
从而 .
.
因为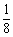 ,
,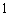 ,
,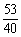 同时属于
同时属于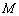 ,所以存在三个不同的整数
,所以存在三个不同的整数 (
( ),
),
使得 从而
从而
则  .
.
因为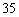 与
与 互质,且
互质,且 与
与 为整数,
为整数,
所以 ,但
,但 ,矛盾.
,矛盾.
所以不存在实数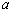 ,
,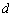 ,使
,使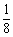 ,
,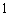 ,
,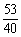 都属于
都属于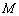 .
.

练习册系列答案
相关题目
某学生对一些对数进行运算,如下图表格所示:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
现在发觉学生计算中恰好有两次地方出错,那么出错的数据是 ( )
A.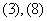 B.
B.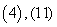 C.
C.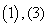 D.
D.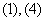
 ,若
,若 ,则
,则 ;若
;若 ,则
,则 的导函数是
的导函数是 ,则
,则 __________.
__________.





 (1)
(1) (2)
(2) (3)
(3) (4)
(4)



 (5)
(5) (6)
(6) (7)
(7) (8)
(8)


 (9)
(9) (10)
(10) (11)
(11) 满足
满足 ,则
,则 的最小值为 .
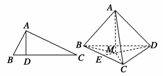
的最小值为 . 在正方形
在正方形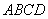 所在平面外,
所在平面外, ,
, 与
与 所成角的大小为( )
所成角的大小为( ) B.
B. C.
C. D.
D.
 且
且 ,则使不等式
,则使不等式 恒成立的实数
恒成立的实数 的取值范围__________________.
的取值范围__________________.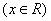 满足f(
满足f(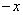 )=f(x),f(x)=f(2
)=f(x),f(x)=f(2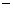 x),且当
x),且当 时,f(x)=x3.又函数g(x)=|xcos
时,f(x)=x3.又函数g(x)=|xcos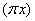 |,则函数h(x)=g(x)-f(x)在
|,则函数h(x)=g(x)-f(x)在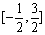 上的零点个数为
上的零点个数为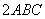 =S△BCM·S△BCD.上述命题是( )
=S△BCM·S△BCD.上述命题是( )