题目内容
已知关于x的方程x2+（2+a）x+1+a+b=0的两根为x1，x2，且0＜x1＜1＜x2，则z=
的取值范围是
| a+b |
| a-b |
(-
，
)
| 1 |
| 3 |
| 1 |
| 5 |
(-
，
)
．| 1 |
| 3 |
| 1 |
| 5 |
分析：由题意可得
，即
，如图所示，由图可知
∈(-2，-
)，再由z=
=
在区间(-2，-
)上是增函数，求出z的范围．
|
|
| b |
| a |
| 2 |
| 3 |
| a+b |
| a-b |
1+
| ||
1-
|
| 2 |
| 3 |
解答：解：由方程x2+（2+a）x+1+a+b=0的二次项系数为1＞0，故函数f（x）=x2+（1+a）x+1+a+b图象开口方向朝上．
又∵方程x2+（1+a）x+1+a+b=0的两根满足0＜x1＜1＜x2，则
，
即
，即
，如图所示：
∵
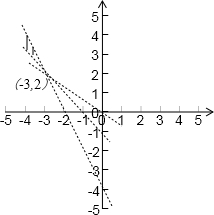
表示阴影区域上一点与原点连线的斜率，由图可知
∈(-2，-
)，
而z=
=
在区间(-2，-
)上是增函数，
而当
=-2时，z=-
，当
=-
时，z=
，
则z=
的取值范围是 (-
，
)，
故答案：(-
，
)．
又∵方程x2+（1+a）x+1+a+b=0的两根满足0＜x1＜1＜x2，则
|
即
|
|
∵
| b |
| a |
| b |
| a |
| 2 |
| 3 |
而z=
| a+b |
| a-b |
1+
| ||
1-
|
| 2 |
| 3 |
而当
| b |
| a |
| 1 |
| 3 |
| b |
| a |
| 2 |
| 3 |
| 1 |
| 5 |
则z=
| a+b |
| a-b |
| 1 |
| 3 |
| 1 |
| 5 |
故答案：(-
| 1 |
| 3 |
| 1 |
| 5 |
点评：本题主要考查一元二次方程根的分布与系数的关系，体现了转化、数形结合的数学思想，属于中档题
练习册系列答案
相关题目