题目内容
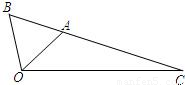
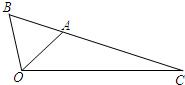 如图,△OAB是等边三角形,∠AOC=45°,OC=
如图,△OAB是等边三角形,∠AOC=45°,OC=| 2 |
(Ⅰ)求sin∠BOC的值;
(Ⅱ)求线段BC的长.
分析:(Ⅰ)根据△OAB是等边三角形和∠AOC的值,可确定∠BOC的值,再由两角和与差的正弦公式可得到答案.
(Ⅱ)在△OCB中应用正弦定理得到BC=sin∠BOC•
,然后将sin∠BOC、OC、sin∠OBC的值代入即可得到答案.
(Ⅱ)在△OCB中应用正弦定理得到BC=sin∠BOC•
| OC |
| sin∠OBC |
解答:解:(Ⅰ)∵△OAB是等边三角形,∠AOC=45°∴∠BOC=45°+60°
∴sin∠BOC=sin(45°+60°)=sin45°cos60°=
(Ⅱ)在△OCB中,∵
=
∴BC=sin∠BOC•
=
•
=1+
.
∴sin∠BOC=sin(45°+60°)=sin45°cos60°=
| ||||
| 4 |
(Ⅱ)在△OCB中,∵
| OC |
| sin∠OBC |
| BC |
| sin∠BOC |
∴BC=sin∠BOC•
| OC |
| sin∠OBC |
| ||||
| 4 |
| ||
| sin60° |
| ||
| 3 |
点评:本题主要考查两角和与差的公式、正弦定理的应用.考查对三角函数的公式的记忆和理解程度,三角函数的公式比较多,不容易记,一定要在平时就注意积累,这样到考试是才不会手忙脚乱.

练习册系列答案
相关题目
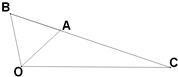 如图,△OAB是等边三角形,∠AOC=45°,
如图,△OAB是等边三角形,∠AOC=45°,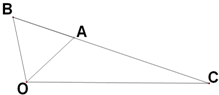 如图,△OAB是等边三角形,∠AOC=45°,OC=
如图,△OAB是等边三角形,∠AOC=45°,OC=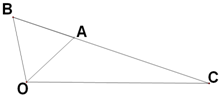
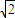 ,A、B、C三点共线.
,A、B、C三点共线.