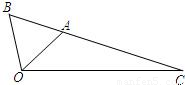
题目内容
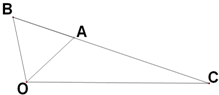如图，△OAB是等边三角形，∠AOC=45°，OC=| 2 |
（1）求
| OB |
| BC |
（2）D是线段BC上的任意点，若
| OD |
| OB |
| OC |
分析：（1）先利用和差角公式求出sin15°，然后在△OAC中，利用正弦定理可求OA，AC，结合已知条件求出BC=AC+AB，及
与
的夹角，再结合向量的数量积的定义可求
（2）由D，B，C三点共线可设
=λ
（0≤λ≤1），从而可得
=(1-λ)
+λ
，结合
=x
+y
，
可得x，y与λ的关系，结合基本不等式（或二次函数的性质可求xy的最大值
| OB |
| OC |
（2）由D，B，C三点共线可设
| CD |
| CB |
| OD |
| OC |
| OB |
| OD |
| OB |
| OC |
可得x，y与λ的关系，结合基本不等式（或二次函数的性质可求xy的最大值
解答：解：（1）sin15o=sin(45o-30o)=
，
在△OAC中，
=
=
，
=
=
=
故OA=
sin15o=
×
=1-
，
AC=
sin45o=
×
=
，
∵OA=AB=OB=1-
，
故BC=AC+AB=1+
，∠OBC=60°可得＜
，
＞=120°
∴
•
=（1-
)(1+
)×cos120°（1+
×（cos120°）-
（2）∵D，B，C三点共线
故可设
=λ
（0≤λ≤1）
=(1-λ)
+λ
∵
=x
+y
，
故x+y=λ+（1-λ）=1，（其中0≤x≤1，0≤y≤1）
令f(x)=xy=x(1-x)≤(
)2=
(0≤x≤1)或二次函数法．（13分）
| ||||
| 4 |
在△OAC中，
| OC |
| sin120o |
| OA |
| sin15o |
| AC |
| sin45o |
| ||||
|
2
| ||
| 3 |
| OA |
| sin15o |
| AC |
| sin45o |
故OA=
2
| ||
| 3 |
2
| ||
| 3 |
| ||||
| 4 |
| ||
| 3 |
AC=
2
| ||
| 3 |
2
| ||
| 3 |
| ||
| 2 |
2
| ||
| 3 |
∵OA=AB=OB=1-
| ||
| 3 |
故BC=AC+AB=1+
| ||
| 3 |
| OB |
| OC |
∴
| OB |
| OC |
| ||
| 3 |
| ||
| 3 |
| ||
| 3 |
| 1 |
| 3 |
（2）∵D，B，C三点共线
故可设
| CD |
| CB |
| OD |
| OC |
| OB |
∵
| OD |
| OB |
| OC |
故x+y=λ+（1-λ）=1，（其中0≤x≤1，0≤y≤1）
令f(x)=xy=x(1-x)≤(
| x+1-x |
| 2 |
| 1 |
| 4 |
点评：本题主要考查了正弦定理在求解三角形中的应，还考查了向量的数量积及向量共线定理的应用．
练习册系列答案
阅读快车系列答案
相关题目
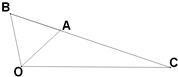如图，△OAB是等边三角形，∠AOC=45°，
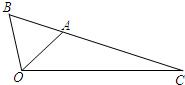如图，△OAB是等边三角形，∠AOC=45°，OC=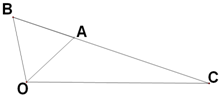
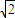，A、B、C三点共线．