题目内容
已知f(x)=xlnx,g(x)= x3-x2-ax+2.
x3-x2-ax+2.(1)求函数f(x)的单调区间;
(2)若对任意x∈(0,+∞),g′(x)≥f(e)恒成立,求实数a的取值范围.
【答案】分析:(1)求出原函数的导函数,由导函数等于0得到导函数的零点,由导函数的零点对定义域分段后判断在不同区间内导函数的符号,从而求得函数f(x)的单调区间;
(2)求出函数g(x)的导函数,配方后求出导函数的最小值,代入g′(x)≥f(e)后分离变量即可得到实数a的取值范围.
解答:解:(1)由f(x)=xlnx,得f′(x)=lnx+1.
令f′(x)>0,得lnx>-1,∴x>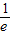 .
.
由于f(x)的定义域为(0,+∞),
∴f(x)在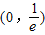 上单调递减,在
上单调递减,在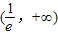 单调递增;
单调递增;
(2)由g(x)= x3-x2-ax+2.
x3-x2-ax+2.
所以g′(x)=x2-2x-a=(x-1)2-1-a.
则g′(x)min=-1-a.
由g′(x)≥f(e)恒成立,
得-1-a≥f(e)=e恒成立,
∴a≤-1-e.
点评:本题考查了利用导数研究函数的单调性,考查了利用配方法求函数的最值,训练了分离变量法,是中档题.
(2)求出函数g(x)的导函数,配方后求出导函数的最小值,代入g′(x)≥f(e)后分离变量即可得到实数a的取值范围.
解答:解:(1)由f(x)=xlnx,得f′(x)=lnx+1.
令f′(x)>0,得lnx>-1,∴x>
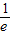 .
.由于f(x)的定义域为(0,+∞),
∴f(x)在
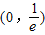 上单调递减,在
上单调递减,在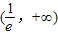 单调递增;
单调递增;(2)由g(x)=
 x3-x2-ax+2.
x3-x2-ax+2.所以g′(x)=x2-2x-a=(x-1)2-1-a.
则g′(x)min=-1-a.
由g′(x)≥f(e)恒成立,
得-1-a≥f(e)=e恒成立,
∴a≤-1-e.
点评:本题考查了利用导数研究函数的单调性,考查了利用配方法求函数的最值,训练了分离变量法,是中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目