题目内容
（本小题10分）
在极坐标系下，已知圆
的圆心为
，且过极点
．
（Ⅰ）写出圆的极坐标方程；
（Ⅱ）已知直线
过极点且与圆相交的弦长为
，求直线的极坐标方程．
（本小题10分）
解：（Ⅰ）圆
的极坐标方程为：
； ………………………… 4分
（Ⅱ）法一：设直线
的极坐标方程为
（
R），代入圆方程，得
，
弦长为
，
或
，
Z
不妨取
和
， …………………………8分
直线的极坐标方程为
（R）或
（R）．…10分
法二：圆的直角坐标方程为：
①当
存在时，设直线
则圆心到直线的距离
，
，
此时直线的极坐标方程为（R）；
②当不存在时，则圆心到直线的距离
，也满足．
此时直线的极坐标方程为（R）．
综上，直线的极坐标方程为（R）或（R）．
练习册系列答案
习题精选系列答案
相关题目
中，
，
，前
项和
，求项数
的值。
（元）的概率分布列和期望
.
中， 
分别是
的对边，
是方程
的两个根，且
．
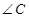的度数和
的长度．
上的一个动点，求S=x+y的最大值。