题目内容
15.函数f(x)=$\left\{\begin{array}{l}{f(x+2),x<2}\\{{2}^{-x},x≥2}\end{array}\right.$,则f(0)=( )| A. | 4 | B. | 8 | C. | $\frac{1}{8}$ | D. | $\frac{1}{4}$ |
分析 直接利用分段函数化简求解即可.
解答 解:函数f(x)=$\left\{\begin{array}{l}{f(x+2),x<2}\\{{2}^{-x},x≥2}\end{array}\right.$,则f(0)=f(2)=2-2=$\frac{1}{4}$.
故选:D.
点评 本题考查分段函数的应用,函数值的求法,考查计算能力.

练习册系列答案
相关题目
10.在平行四边形ABCD中,$\overrightarrow{AB}$=(cos18°,cos72°),$\overrightarrow{BC}$=(2cos63°,2cos27°),则四边形ABCD的面积为( )
| A. | $\frac{\sqrt{2}}{4}$ | B. | $\sqrt{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{2}}{2}$ |
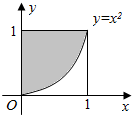 如图所示,曲线y=x2与y轴、直线y=1围成区域A(图中阴影部分),用模拟的方法求图中阴影部分的面积.(用两种方法)
如图所示,曲线y=x2与y轴、直线y=1围成区域A(图中阴影部分),用模拟的方法求图中阴影部分的面积.(用两种方法)