题目内容
已知椭圆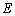 的中心在坐标原点,焦点在坐标轴上,且经过
的中心在坐标原点,焦点在坐标轴上,且经过 、
、 、
、 三点.
三点.
(1)求椭圆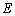 的方程;
的方程;
(2)若点D为椭圆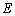 上不同于
上不同于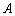 、
、 的任意一点,
的任意一点, ,
, ,求当
,求当 内切圆的面积最大时内切圆圆心的坐标;
内切圆的面积最大时内切圆圆心的坐标;
(3)若直线 :
: 与椭圆
与椭圆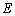 交于
交于 、
、 两点,证明直线
两点,证明直线 与
与 的交点在直线
的交点在直线 上.
上.
(1)设椭圆方程为 ,
,
将 、
、 、
、 代入椭圆E的方程,得
代入椭圆E的方程,得
 ,解得
,解得 ,
, .
.
∴椭圆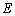 的方程
的方程 .
.

故内切圆圆心的坐标为 .
.
(3)解法一:将直线 代入椭圆
代入椭圆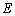 的方程
的方程 并整理得
并整理得
 .
.
设直线 与椭圆
与椭圆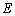 的交点
的交点 ,
, .
.
由韦达定理得 ,
, .
.
直线 的方程为
的方程为 ,它与直线
,它与直线 的交点坐标为
的交点坐标为 ,
,
同理可求得直线 与直线
与直线 的交点坐标为
的交点坐标为 .
.
下面证明 、
、 两点重合,即证明
两点重合,即证明 、
、 两点的纵坐标相等.
两点的纵坐标相等.
∵ ,
,
∴

因此结论成立.
综上可知直线 与直线
与直线 的交点住直线
的交点住直线 上.
上.
解法二:直线 的方程为
的方程为 ,即
,即 .
.
由直线 的方程为
的方程为 ,即
,即
由直线 与直线
与直线 的方程消去
的方程消去 ,得
,得


故直线 与直线
与直线 的交点在直线
的交点在直线 上.
上.

练习册系列答案
相关题目
 、m、n是互不相同的空间直线,α、β是不重合的平面,则下列命题中为真命题的是( )
、m、n是互不相同的空间直线,α、β是不重合的平面,则下列命题中为真命题的是( )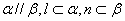 ,则
,则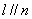 B.若
B.若 ,则
,则
 ,则
,则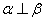 D.若
D.若 ,则
,则
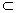
 ,给出以下四个命题:
,给出以下四个命题: ,则直线a//平面
,则直线a//平面 的离心率为
的离心率为 ,右焦点为
,右焦点为 ,方程
,方程 的两个实根分别为
的两个实根分别为 和
和 ,则点
,则点 ( )
( ) 上 B.必在圆
上 B.必在圆 的椭圆C:
的椭圆C: 和双曲线
和双曲线 的离心率互为倒
的离心率互为倒 ,且
,且 与椭圆的公共
与椭圆的公共 。数列{ bn} 满足
。数列{ bn} 满足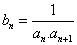 为数列{ bn} 的前n项和。
为数列{ bn} 的前n项和。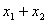 =6,那么
=6,那么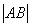 = ( )
= ( )  ,则
,则 的大小关系是
的大小关系是 B.
B. C.
C. D.
D.