题目内容
如图,抛物线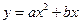 (a
(a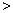 0)与双曲线
0)与双曲线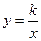 相交于点A,B. 已知点A的坐标为(1,4),点B在第三象限内,且△AOB的面积为3(O为坐标原点).
相交于点A,B. 已知点A的坐标为(1,4),点B在第三象限内,且△AOB的面积为3(O为坐标原点).
(1)求实数a,b,k的值;
(2)过抛物线上点A作直线AC∥x轴,交抛物线于另一点C,求所有满足△EOC∽△AOB的点E的坐标.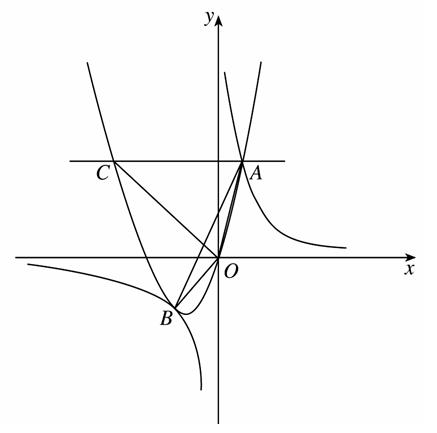
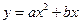 (a
(a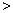 0)与双曲线
0)与双曲线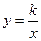 相交于点A,B. 已知点A的坐标为(1,4),点B在第三象限内,且△AOB的面积为3(O为坐标原点).
相交于点A,B. 已知点A的坐标为(1,4),点B在第三象限内,且△AOB的面积为3(O为坐标原点).(1)求实数a,b,k的值;
(2)过抛物线上点A作直线AC∥x轴,交抛物线于另一点C,求所有满足△EOC∽△AOB的点E的坐标.

解:(1)因为点A(1,4)在双曲线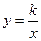 上,
上,
所以k="4." 故双曲线的函数表达式为 . ……………………..2分
. ……………………..2分
设点B(t, ),
), ,AB所在直线的函数表达式为
,AB所在直线的函数表达式为 ,则有
,则有
 解得
解得 ,
, ……………..4分
……………..4分
于是,直线AB与y轴的交点坐标为 ,…………………..5分
,…………………..5分
故 ,整理得
,整理得 ,
,
解得 ,或t=
,或t= (舍去).所以点B的坐标为(
(舍去).所以点B的坐标为( ,
, ).…………………..8分
).…………………..8分
因为点A,B都在抛物线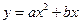 (a
(a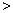 0)上,所以
0)上,所以
解得 …………10分
…………10分
(2)如图,因为AC∥x轴,所以C( ,4),于是CO=4
,4),于是CO=4 . 又BO=2
. 又BO=2 ,所以
,所以 .
.

设抛物线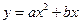 (a
(a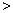 0)与x轴负半轴相交于点D,则点D的坐标为(
0)与x轴负半轴相交于点D,则点D的坐标为( ,0).
,0).
因为∠COD=∠BOD= ,所以∠COB=
,所以∠COB= . …………12分
. …………12分
(i)将△ 绕点O顺时针旋转
绕点O顺时针旋转 ,得到△
,得到△ .这时,点
.这时,点 (
( ,2)是CO的中点,点
,2)是CO的中点,点 的坐标为(4,
的坐标为(4, ).
).
延长 到点
到点 ,使得
,使得 =
= ,这时点
,这时点 (8,
(8, )是符合条件的点. …………16分(ii)作△
)是符合条件的点. …………16分(ii)作△ 关于x轴的对称图形△
关于x轴的对称图形△ ,得到点
,得到点 (1,
(1, );延长
);延长 到点
到点 ,使得
,使得 =
= ,这时点E2(2,
,这时点E2(2, )是符合条件的点.
)是符合条件的点.
所以,点 的坐标是(8,
的坐标是(8, ),或(2,
),或(2, ). …………20分
). …………20分
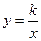 上,
上,所以k="4." 故双曲线的函数表达式为
 . ……………………..2分
. ……………………..2分设点B(t,
 ),
), ,AB所在直线的函数表达式为
,AB所在直线的函数表达式为 ,则有
,则有 解得
解得 ,
, ……………..4分
……………..4分于是,直线AB与y轴的交点坐标为
 ,…………………..5分
,…………………..5分故
 ,整理得
,整理得 ,
,解得
 ,或t=
,或t= (舍去).所以点B的坐标为(
(舍去).所以点B的坐标为( ,
, ).…………………..8分
).…………………..8分因为点A,B都在抛物线
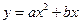 (a
(a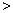 0)上,所以
0)上,所以
解得
 …………10分
…………10分(2)如图,因为AC∥x轴,所以C(
 ,4),于是CO=4
,4),于是CO=4 . 又BO=2
. 又BO=2 ,所以
,所以 .
.
设抛物线
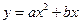 (a
(a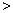 0)与x轴负半轴相交于点D,则点D的坐标为(
0)与x轴负半轴相交于点D,则点D的坐标为( ,0).
,0).因为∠COD=∠BOD=
 ,所以∠COB=
,所以∠COB= . …………12分
. …………12分(i)将△
 绕点O顺时针旋转
绕点O顺时针旋转 ,得到△
,得到△ .这时,点
.这时,点 (
( ,2)是CO的中点,点
,2)是CO的中点,点 的坐标为(4,
的坐标为(4, ).
).延长
 到点
到点 ,使得
,使得 =
= ,这时点
,这时点 (8,
(8, )是符合条件的点. …………16分(ii)作△
)是符合条件的点. …………16分(ii)作△ 关于x轴的对称图形△
关于x轴的对称图形△ ,得到点
,得到点 (1,
(1, );延长
);延长 到点
到点 ,使得
,使得 =
= ,这时点E2(2,
,这时点E2(2, )是符合条件的点.
)是符合条件的点.所以,点
 的坐标是(8,
的坐标是(8, ),或(2,
),或(2, ). …………20分
). …………20分略

练习册系列答案
相关题目
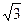 )的直线l过点(0,-2
)的直线l过点(0,-2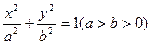
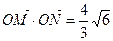 cot∠MON ≠0(O为原点).若存在,求直线m的方程;若不存
cot∠MON ≠0(O为原点).若存在,求直线m的方程;若不存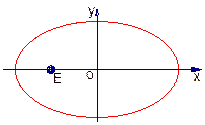
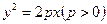 的焦点,斜率为
的焦点,斜率为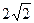 的直线交抛物线于
的直线交抛物线于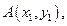
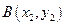 (
(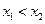 )两点,且
)两点,且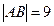
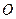 为坐标原点,
为坐标原点,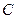 为抛物线上一点,若
为抛物线上一点,若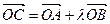 ,求
,求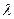 的值
的值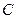 的右焦点为
的右焦点为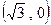 ,离心率为
,离心率为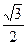
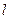 :
: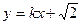 与椭圆
与椭圆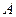 、
、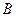 ,且
,且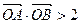 (其中
(其中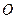 为原点),求实数
为原点),求实数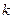 的取值范围
的取值范围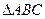 中,
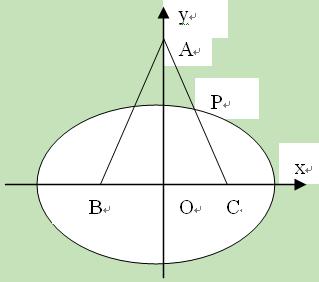
中,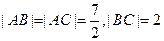 ,以
,以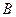 、
、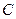 为焦点的椭圆恰好过
为焦点的椭圆恰好过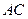 的中点
的中点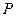 。
。
 作直线
作直线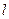 与圆
与圆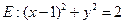 相交于
相交于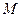 、
、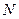 两点,试探究点
两点,试探究点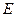 分割成弧长比值为
分割成弧长比值为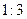 的两段弧吗?若能,求出直线
的两段弧吗?若能,求出直线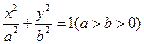 的左、右焦点分别为F1、F2.F2也是抛物线C2:
的左、右焦点分别为F1、F2.F2也是抛物线C2: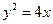 的焦点,点M为C1与C2在第一象限的交点,且
的焦点,点M为C1与C2在第一象限的交点,且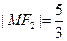 .
.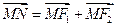 ,直线l∥MN,且与C1交于A、B两点,若
,直线l∥MN,且与C1交于A、B两点,若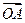 ·
·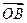 =0,求直线l的方程.
=0,求直线l的方程.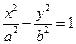 的渐近线为
的渐近线为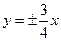 ,则双曲线的离心率为___________.
,则双曲线的离心率为___________.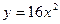 的焦点坐标为 。
的焦点坐标为 。