题目内容
已知直角坐标系中三点A（3，0），B（0，3），C（cosα，sinα），且
•
=-1，求sin2α的值．
| AC |
| BC |
∵A（3，0），B（0，3），C（cosα，sinα），
∴
=（ cosα-3，sinα），
=（cosα，sinα-3），
∴
•
=（ cosα-3，sinα）•（cosα，sinα-3）
=（ cosα-3）cosα+sinα（ sinα-3）=-1，
∴cos2α+sin2α-3 cosα-3 sinα=-1
即sinα+cosα=
，∴（sinα+cosα）2=（
）2
cos2α+sin2α+2cosα•sinα=
，∴sin2α=-
．
∴
| AC |
| BC |
∴
| AC |
| BC |
=（ cosα-3）cosα+sinα（ sinα-3）=-1，
∴cos2α+sin2α-3 cosα-3 sinα=-1
即sinα+cosα=
| 2 |
| 3 |
| 2 |
| 3 |
cos2α+sin2α+2cosα•sinα=
| 4 |
| 9 |
| 5 |
| 9 |
练习册系列答案
阅读快车系列答案
相关题目
已知平面直角坐标系中三点坐标分别为A（3，0），B（0，4），C（cosθ，sinθ），θ∈R，则△ABC面积的最大值为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
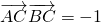，求sin2α的值．
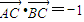，求sin2α的值．