题目内容
已知直角坐标系中三点A(3,0),B(0,3),C(cosα,sinα),且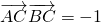 ,求sin2α的值.
,求sin2α的值.
解:∵A(3,0),B(0,3),C(cosα,sinα),
∴ =( cosα-3,sinα),
=( cosα-3,sinα), =(cosα,sinα-3),
=(cosα,sinα-3),
∴ •
• =( cosα-3,sinα)•(cosα,sinα-3)
=( cosα-3,sinα)•(cosα,sinα-3)
=( cosα-3)cosα+sinα( sinα-3)=-1,
∴cos2α+sin2α-3 cosα-3 sinα=-1
即sinα+cosα= ,∴(sinα+cosα)2=(
,∴(sinα+cosα)2=( )2
)2
cos2α+sin2α+2cosα•sinα= ,∴sin2α=-
,∴sin2α=- .
.
分析:根据题意和坐标运算求出 和
和 的坐标,再由数量积的坐标运算,代入
的坐标,再由数量积的坐标运算,代入 •
• =-1列出方程,利用平方关系求出sinα+cosα的值,两边平方后由二倍角的正弦公式求出.
=-1列出方程,利用平方关系求出sinα+cosα的值,两边平方后由二倍角的正弦公式求出.
点评:本题是有关向量和三角函数的综合题,也是高考的常考题型,利用向量的坐标运算列出方程,再利用三角变换的公式进行化简求值.
∴
 =( cosα-3,sinα),
=( cosα-3,sinα), =(cosα,sinα-3),
=(cosα,sinα-3),∴
 •
• =( cosα-3,sinα)•(cosα,sinα-3)
=( cosα-3,sinα)•(cosα,sinα-3)=( cosα-3)cosα+sinα( sinα-3)=-1,
∴cos2α+sin2α-3 cosα-3 sinα=-1
即sinα+cosα=
 ,∴(sinα+cosα)2=(
,∴(sinα+cosα)2=( )2
)2cos2α+sin2α+2cosα•sinα=
 ,∴sin2α=-
,∴sin2α=- .
.分析:根据题意和坐标运算求出
 和
和 的坐标,再由数量积的坐标运算,代入
的坐标,再由数量积的坐标运算,代入 •
• =-1列出方程,利用平方关系求出sinα+cosα的值,两边平方后由二倍角的正弦公式求出.
=-1列出方程,利用平方关系求出sinα+cosα的值,两边平方后由二倍角的正弦公式求出.点评:本题是有关向量和三角函数的综合题,也是高考的常考题型,利用向量的坐标运算列出方程,再利用三角变换的公式进行化简求值.

练习册系列答案
相关题目
已知平面直角坐标系中三点坐标分别为A(3,0),B(0,4),C(cosθ,sinθ),θ∈R,则△ABC面积的最大值为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
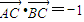 ,求sin2α的值.
,求sin2α的值.