题目内容
已知圆O的半径为1,PA、PB为该圆的两条切线,A、B为俩切点,那么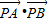 的最小值为( )
的最小值为( )A.
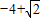
B.
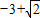
C.
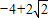
D.
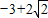
【答案】分析:要求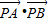 的最小值,我们可以根据已知中,圆O的半径为1,PA、PB为该圆的两条切线,A、B为俩切点,结合切线长定理,设出PA,PB的长度,和夹角,并将
的最小值,我们可以根据已知中,圆O的半径为1,PA、PB为该圆的两条切线,A、B为俩切点,结合切线长定理,设出PA,PB的长度,和夹角,并将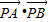 表示成一个关于X的函数,然后根据求函数最值的办法,进行解答.
表示成一个关于X的函数,然后根据求函数最值的办法,进行解答.
解答: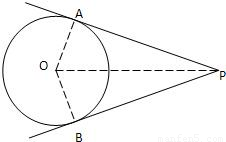 解:如图所示:设PA=PB=x(x>0),
解:如图所示:设PA=PB=x(x>0),
∠APO=α,则∠APB=2α,
PO=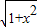 ,
,
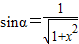 ,
,
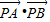 =
=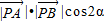
=x2(1-2sin2α)
=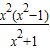
=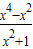 ,
,
令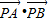 =y,则
=y,则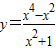 ,
,
即x4-(1+y)x2-y=0,由x2是实数,
所以△=[-(1+y)]2-4×1×(-y)≥0,y2+6y+1≥0,
解得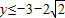 或
或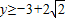 .
.
故(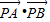 )min=-3+2
)min=-3+2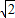 .此时
.此时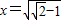 .
.
点评:本小题主要考查向量的数量积运算与圆的切线长定理,着重考查最值的求法--判别式法,同时也考查了考生综合运用数学知识解题的能力及运算能力.
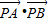 的最小值,我们可以根据已知中,圆O的半径为1,PA、PB为该圆的两条切线,A、B为俩切点,结合切线长定理,设出PA,PB的长度,和夹角,并将
的最小值,我们可以根据已知中,圆O的半径为1,PA、PB为该圆的两条切线,A、B为俩切点,结合切线长定理,设出PA,PB的长度,和夹角,并将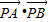 表示成一个关于X的函数,然后根据求函数最值的办法,进行解答.
表示成一个关于X的函数,然后根据求函数最值的办法,进行解答.解答:
 解:如图所示:设PA=PB=x(x>0),
解:如图所示:设PA=PB=x(x>0),∠APO=α,则∠APB=2α,
PO=
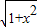 ,
,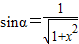 ,
,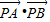 =
=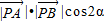
=x2(1-2sin2α)
=
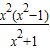
=
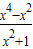 ,
,令
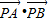 =y,则
=y,则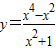 ,
,即x4-(1+y)x2-y=0,由x2是实数,
所以△=[-(1+y)]2-4×1×(-y)≥0,y2+6y+1≥0,
解得
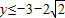 或
或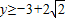 .
.故(
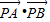 )min=-3+2
)min=-3+2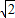 .此时
.此时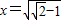 .
.点评:本小题主要考查向量的数量积运算与圆的切线长定理,着重考查最值的求法--判别式法,同时也考查了考生综合运用数学知识解题的能力及运算能力.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目
已知圆O的半径为1,PA、PB为该圆的两条切线,A、B为两切点,那么
•
的最小值为( )
| PA |
| PB |
A、-4+
| ||
B、-3+
| ||
C、-4+2
| ||
D、-3+2
|