题目内容
如图,有一个以圆心角为60°,半径为
km的扇形湖面AOB.现欲在弧AB上任取一点P,作扇形的内接矩形PNMQ,使点Q在半径OA上,点N,M在半径OB上,将该扇形湖面内隔为四个养殖区域.设矩形PNMQ区域的面积为y;
(1)当∠POB=45°时,求矩形PNMQ的面积;
(2)设∠POB=θ,将y表示成θ的函数关系式,并求出y的最大值.

| 3 |
(1)当∠POB=45°时,求矩形PNMQ的面积;
(2)设∠POB=θ,将y表示成θ的函数关系式,并求出y的最大值.

分析:(1)分别计算MN、PN,即可求得矩形的面积=MN×PN;
(2)计算PN、MN的长,从而可得面积表达式,再利用辅助角公式化简函数,利用角的范围,即可求得面积的最大值.
(2)计算PN、MN的长,从而可得面积表达式,再利用辅助角公式化简函数,利用角的范围,即可求得面积的最大值.
解答: 解:(1)当∠POB=45°时,∵PO=
解:(1)当∠POB=45°时,∵PO=
,
∴PN=
sin45°=
,ON=
cos45°=
,
又OM=QMtan30°=
×
=
,
∴MN=ON-OM=
,…(3分),
所以矩形的面积=MN×PN=
×
=
.…(5分)
(2)因为PN=
sinθ,ON=
cosθ,OM=
×
sinθ=sinθ,
所以MN=ON-OM=
cosθ-sinθ…(7分)
∴y=
sinθ(
cosθ-sinθ),即y=3sinθcosθ-
sin2θ,(θ∈(0,
))(9分)
∴y=3sinθcosθ-
sin2θ=
sin(2θ+
)-
,…(12分)
∵θ∈(0,
),∴2θ+
∈(
,
)…(13分)
所以ymax=
.…(14分)
 解:(1)当∠POB=45°时,∵PO=
解:(1)当∠POB=45°时,∵PO=| 3 |
∴PN=
| 3 |
| ||
| 2 |
| 3 |
| ||
| 2 |
又OM=QMtan30°=
| ||
| 2 |
| ||
| 3 |
| ||
| 2 |
∴MN=ON-OM=
| ||||
| 2 |
所以矩形的面积=MN×PN=
| ||||
| 2 |
| ||
| 2 |
3-
| ||
| 2 |
(2)因为PN=
| 3 |
| 3 |
| ||
| 3 |
| 3 |
所以MN=ON-OM=
| 3 |
∴y=
| 3 |
| 3 |
| 3 |
| π |
| 3 |
∴y=3sinθcosθ-
| 3 |
| 3 |
| π |
| 6 |
| ||
| 2 |
∵θ∈(0,
| π |
| 3 |
| π |
| 6 |
| π |
| 6 |
| 5π |
| 6 |
所以ymax=
| ||
| 2 |
点评:本题考查矩形面积的计算,考查三角函数知识,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
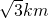 的扇形湖面AOB.现欲在弧AB上任取一点P,作扇形的内接矩形PNMQ,使点Q在半径OA上,点N,M在半径OB上,将该扇形湖面内隔为四个养殖区域.设矩形PNMQ区域的面积为y;
的扇形湖面AOB.现欲在弧AB上任取一点P,作扇形的内接矩形PNMQ,使点Q在半径OA上,点N,M在半径OB上,将该扇形湖面内隔为四个养殖区域.设矩形PNMQ区域的面积为y;