题目内容
若直线 (
( )被圆
)被圆 截得的弦长为4,则
截得的弦长为4,则 的最小值为( )
的最小值为( )
A. | B. | C.2 | D.4 |
D
解析试题分析:易知圆心为(-1,2),圆的半径为2,因为直线被圆截得的弦长为4,所以直线过圆心,所以-2a-2b+2=0,即a+b=1。又 ,
,
所以 。
。
考点:直线与圆的位置关系;基本不等式;点到直线的距离公式。
点评:做本题的关键是灵活应用“1”代换,使 变形为
变形为 ,从而就达到积为定值的目的,应用基本不等式。“1”代换是我们常用的方法,我们要注意熟练掌握。
,从而就达到积为定值的目的,应用基本不等式。“1”代换是我们常用的方法,我们要注意熟练掌握。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
设 、
、 为正数,则
为正数,则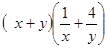 的最小值为( )
的最小值为( )
A. | B.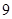 | C.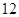 | D. |
若函数f(x)=x+ (x>2)在
(x>2)在 处取最小值,则
处取最小值,则
A. | B. | C.3 | D.4 |
若正数 满足
满足 ,则
,则 的最小值是( )
的最小值是( )
A. | B. | C. | D. |
已知点(x,y)在直线x+2y=3上移动,则2x+4y的最小值是( )
| A.8 | B.6 | C.3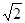 | D.4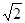 |
若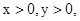 且
且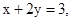 则
则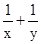 的最小值为( )
的最小值为( )
A.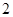 | B.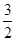 | C.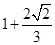 | D. |
设 ,若
,若 ,且
,且 ,则
,则 的取值范围是( )
的取值范围是( )
A. | B. | C. | D. |
已知 为正实数,且
为正实数,且 ,若
,若 对于满足条件的
对于满足条件的 恒成立,则
恒成立,则 的取值范围为
的取值范围为
A. | B. | C. | D. |
设 ,则
,则 的最小值是( )
的最小值是( )
| A.2 | B.4 | C. | D.5 |