题目内容
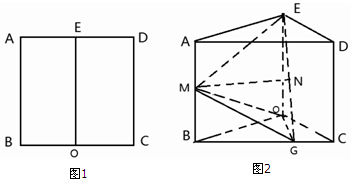
1.如图1,在边长为$2\sqrt{3}$的正方形ABCD中,E、O分别为 AD、BC的中点,沿 EO将矩形ABOE折起使得∠BOC=120°,如图2所示,点G 在BC上,BG=2GC,M、N分别为AB、EG中点.(Ⅰ)求证:MN∥平面OBC;
(Ⅱ)求二面角 G-ME-B的余弦值.
分析 (Ⅰ)法一:取OG中点F,连结BF、FN,证明MN∥BF,然后证明MN∥平面OBC.法二:延长EM、OB交于点Q,连结GQ,证明M为EQ中点,推出MN∥QG,然后证明MN∥平面OBC.
(Ⅱ)法一:证明OG⊥OB,推出OE⊥平面OBC,证明OE⊥OG,然后推出OG⊥QE,说明∠OMG为二面角G-ME-B的平面角,Rt△MOG中,求解即可.
法二:建立空间直角坐标系O-xyz,求出面BOE的一个法向量,平面MGE的法向量,利用空间向量的数量积求解即可.
解答 (Ⅰ)证明:法一如图13取OG中点F,连结BF、FN,
则中位线FN∥$\frac{1}{2}$OE且FN=$\frac{1}{2}$OE,
又BM∥OE且BM=$\frac{1}{2}$OE …(1分)
所以FN∥BM且FN=BM,所以四边形BFNM是平行四边形,所以MN∥BF,…(2分)
又MN?平面OBC,BF?平面OBC,所以MN∥平面OBC.…(4分)
法二:如图14,延长EM、OB交于点Q,连结GQ,
因为BM∥OE且BM=$\frac{1}{2}$OE,所以$\frac{QM}{QE}=\frac{BM}{OE}=\frac{1}{2}$,
M为EQ中点,…(1分)
所以中位线MN∥QG …(2分)
又MN?平面OBC,QG?面OBC,所以MN∥平面OBC.…(4分)
(Ⅱ)解:法一如图14,因为OB=OC=$\sqrt{3}$,∠BOC=120°,
所以$BC=\sqrt{O{B^2}+O{C^2}-2×OB×OCcos120°}=3$,…(5分)
又BG=2GC.所以$BG=\frac{2}{3}BC=2,GC=1$,$OG=\sqrt{C{G^2}+O{C^2}-2×CG×OCcos30°}=1$,
∴OB2+OG2=BG2,∴∠BOG=90°,OG⊥OB,…(6分)
又∵OE⊥OB,OE⊥OC,OB∩OC=O,
∴OE⊥平面OBC,OG?面OBC,
∴OE⊥OG…(7分)
又OB∩OE=O,所以OG⊥平面OBE,QE?面OBE OG⊥QE,…(8分)
又M为EQ中点,所以OQ=OE=$2\sqrt{3}$,所以OM⊥QE,OM∩OG=O,
所以QE⊥平面OMG,QE⊥MG,∠OMG为二面角G-ME-B的平面角.…(9分)
所以Rt△MOG中,$OM=\sqrt{{{(\sqrt{3})}^2}+{{(\sqrt{3})}^2}}=\sqrt{6}$,$MG=\sqrt{{{(\sqrt{6})}^2}+{1^2}}=\sqrt{7}$,…(11分)$cos∠OMG=\frac{OM}{MG}=\frac{{\sqrt{6}}}{{\sqrt{7}}}=\frac{{\sqrt{42}}}{7}$,∴二面角 G-ME-B的余弦值为$\frac{{\sqrt{42}}}{7}$…(12分)
法二:如图15,∵OB=OC=$\sqrt{3}$,∠BOC=120°,
∴$BC=\sqrt{O{B^2}+O{C^2}-2×OB×OCcos120°}=3$,…(5分)
又BG=2GC,∴$BG=\frac{2}{3}BC=2,GC=1$,$OG=\sqrt{C{G^2}+O{C^2}-2×CG×OCcos30°}=1$,
∴OB2+OG2=BG2,
∴∠BOG=90°,OG⊥OB,…(6分)
又∵OE⊥OB,OE⊥OC,OB∩OC=O,
∴OE⊥平面OBC,OG?面OBC,
∴OE⊥OG…(7分)
又OB∩OE=O,所以OG⊥平面OBE,OE?面OBE,∴OG⊥OE…(8分)
建立如图所示的空间直角坐标系O-xyz,则M($\sqrt{3},0,\sqrt{3})$,G(0,1,0),E($0,0,2\sqrt{3})$,$\overrightarrow{MG}=(-\sqrt{3},1,-\sqrt{3}),\overrightarrow{ME}=(-\sqrt{3},0,\sqrt{3})$,…(9分)
而 $\overrightarrow{n_1}=(0,1,0)$是平面BOE的一个法向量,…(11分)
设平面MGE的法向量为$\overrightarrow{n_2}=(x,y,z)$,
则$\left\{\begin{array}{l}\overrightarrow{n_2}•\overrightarrow{MG}=-\sqrt{3}x+y-\sqrt{3}z=0\\ \overrightarrow{n_2}•\overrightarrow{ME}=-\sqrt{3}x+\sqrt{3}z=0\end{array}\right.$,
令 z=1,则$x=1,y=2\sqrt{3}$,
面MGE的一个法向量为$\overrightarrow{n_2}=(1,2\sqrt{3},1)$,…(10分)
所以$cos<\overrightarrow{n_1},\overrightarrow{n_2}>=\frac{{\overrightarrow{n_1}•\overrightarrow{n_2}}}{{\overrightarrow{|{n_1}}|•\overrightarrow{|{n_2}|}}}=\frac{{2\sqrt{3}}}{{\sqrt{1+12+1}}}=\frac{{2\sqrt{3}}}{{\sqrt{14}}}=\frac{{\sqrt{42}}}{7}$
所以,二面角 G-ME-B的余弦值为$\frac{{\sqrt{42}}}{7}$…(12分)
点评 本题考查直线与平面平行于垂直的判定定理的应用,二面角的平面角的求法,考查空间想象能力以及计算能力.

| A. | {-1,0,1,2} | B. | {-1,0,1} | C. | {-2,-1,0,1} | D. | {-2,-1,0,1,2} |
表1:男生身高频数分布表
| 身高(cm) | [160,165) | [165,170) | [170,175) | [175,180) | [180,185) | [185,190) |
| 频数 | 2 | 5 | 14 | 13 | 4 | 2 |
| 身高(cm) | [150,155) | [155,160) | [160,165) | [165,170) | [170,175) | [175,180) |
| 频数 | 1 | 7 | 12 | 6 | 3 | 1 |
(2)估计该校学生身高在[165,180)的概率;
(3)以样本频率为概率,现从高一年级的男生和女生中分别选出1人,设X表示身高在[165,180)学生的人数,求X的分布列及数学期望.
| A. | $\frac{4}{5}$ | B. | $\frac{3}{5}$ | C. | $\frac{2}{5}$ | D. | $\frac{1}{5}$ |