题目内容
已知函数f（x）＝
, 对任意m∈[－3，3]，不等式f（mx－1）＋f（2x）＜0恒成立，则实数x的取值范围为（ ）
A．（－1，
） B．（－2，
） C．（－2，
） D．（－2，）
【答案】
A
【解析】
试题分析：因为
，故
为奇函数，又
，而
为增函数，故也为增函数，故对任意m∈[－3，3]，不等式f（mx－1）＋f（2x）＜0恒成立，可化为，对任意m∈[－3，3]，不等式
恒成立，即
恒成立，其中
,令
，画出如下图形，只要
的取值在
点横坐标和
点横坐标之间则题意成立，而
，故
，选A.
考点：函数奇偶性增减性、函数构造、数形结合.
练习册系列答案
活力课时同步练习册系列答案
相关题目
．
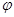）（ω＞0，0＜
＝
，且a∈（0，
），求f（a）的值．
－a
＋x（a＞0）．
＝
，求f（x）图像在x＝1处的切线的方程；
的极大值和极小值分别为m，n，证明：
．
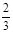与x＝1时都取得极值.
，若f（x）存在零点，则实数a的取值范围