题目内容
已知正项等比数列{an}满足a1a3=16,a5=32
(I)求数列{an}的通项公式;
(II)令bn=log2an,求数列{bn}的前n项和.
解由已知得: ,∵数列为正项数列,∴a2=4,
,∵数列为正项数列,∴a2=4,
设其公比为q,则q3= =8,∴q=2,又
=8,∴q=2,又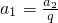 =2,
=2,
∴数列{an}的通项公式an=2•2n-1=2n
(2)由(1)知:bn=log2an=log22n=n,∴bn+1-bn=1
∴数列{bn}是以b1=1为首项,1为公差的等差数列,
∴其前n项和Sn=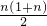
分析:(1)由等比数列的性质和题意可得a2=4,进而可得公比和首项,可得通项公式;
(2)由(1)可得数列{bn}的通项,可知为等差数列,由等差数列的求和公式可得答案.
点评:本题为等差数列好等比数列的综合应用,属基础题.
 ,∵数列为正项数列,∴a2=4,
,∵数列为正项数列,∴a2=4,设其公比为q,则q3=
 =8,∴q=2,又
=8,∴q=2,又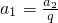 =2,
=2,∴数列{an}的通项公式an=2•2n-1=2n
(2)由(1)知:bn=log2an=log22n=n,∴bn+1-bn=1
∴数列{bn}是以b1=1为首项,1为公差的等差数列,
∴其前n项和Sn=
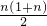
分析:(1)由等比数列的性质和题意可得a2=4,进而可得公比和首项,可得通项公式;
(2)由(1)可得数列{bn}的通项,可知为等差数列,由等差数列的求和公式可得答案.
点评:本题为等差数列好等比数列的综合应用,属基础题.

练习册系列答案
 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
已知正项等比数列{an}中,a1=1,a3a7=4a62,则S6=( )
A、
| ||
B、
| ||
C、
| ||
| D、2 |
已知正项等比数列{an}满足:a7=a6+2a5,若存在两项am,an使得
=4a1,则
+
的最小值为( )
| aman |
| 1 |
| m |
| 1 |
| n |
A、
| ||
B、
| ||
C、
| ||
| D、不存在 |
已知正项等比数列{an}的前n项和为Sn,若S3=3,S9-S6=12,则S6=( )
| A、9 | ||
B、
| ||
| C、18 | ||
| D、39 |