题目内容
 如图,B为△APC的边AC上的一点,且AB=BC=a,∠APB=90°,∠BPC=45°,∠PBA=θ.
如图,B为△APC的边AC上的一点,且AB=BC=a,∠APB=90°,∠BPC=45°,∠PBA=θ.(1)求tanθ的值;
(2)求
| PA |
| PC |
分析:(1)先根据∠APB=90°,AB=a,∠PBA=θ,求PB的值,进而在△BPC中,利用正弦定理求得sinθ=2cosθ.进而求得tanθ的值.
(2)根据(1)中的sinθ=2cosθ,进而根据同角三角函数的基本关系求得sinθ和cosθ的值,进而求得PA和PB,利用余弦定理求得PC,最后根据向量积公式求得答案.
(2)根据(1)中的sinθ=2cosθ,进而根据同角三角函数的基本关系求得sinθ和cosθ的值,进而求得PA和PB,利用余弦定理求得PC,最后根据向量积公式求得答案.
解答:解:(1)∵∠APB=90°,AB=a,∠PBA=θ,∴PB=acosθ.
又在△BPC中,BC=a,∠BPC=45°,∴∠BCP=θ-45°,
∴
=
,∴
=
,
∴sin45°cosθ=sin(θ-45°).∴sinθ=2cosθ.tanθ=2.
(2)由(1)知sinθ=2cosθ,又sin2θ+cos2θ=1
∴sinθ=
,cosθ=
.∴PA=asinθ=
,PB=acosθ=
.
在△BPC中,BC=a,PB=
,
∴PC2=a2+(
)2-2a•
cos(π-θ)=
,∴PC=
.
从而
•
=|
|•|
|cos135°=
•
•(-
)=-
.
又在△BPC中,BC=a,∠BPC=45°,∴∠BCP=θ-45°,
∴
| a |
| sin45° |
| PB |
| sin(θ-45°) |
| a |
| sin45° |
| acosθ |
| sin(θ-45°) |
∴sin45°cosθ=sin(θ-45°).∴sinθ=2cosθ.tanθ=2.
(2)由(1)知sinθ=2cosθ,又sin2θ+cos2θ=1
∴sinθ=
2
| ||
| 5 |
| ||
| 5 |
2
| ||
| 5 |
| ||
| 5 |
在△BPC中,BC=a,PB=
| ||
| 5 |
∴PC2=a2+(
| ||
| 5 |
| ||
| 5 |
| 8a2 |
| 5 |
2
| ||
| 5 |
从而
| PA |
| PC |
| PA |
| PC |
2
| ||
| 5 |
2
| ||
| 5 |
| ||
| 2 |
| 4a2 |
| 5 |
点评:本题主要考查了正弦定理和余弦定理的应用.考查了学生对正弦定理和余弦定理的综合运用.

练习册系列答案
相关题目
 (2013•鹰潭一模)如图,已知三棱锥A-BPC中,AP⊥PC,AC⊥BC,M为AB的中点,D为PB的中点,且△PMB为正三角形.
(2013•鹰潭一模)如图,已知三棱锥A-BPC中,AP⊥PC,AC⊥BC,M为AB的中点,D为PB的中点,且△PMB为正三角形.
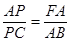
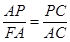
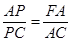 ∵AB=AC
∴
∵AB=AC
∴ 如图,B为△APC的边AC上的一点,且AB=BC=a,∠APB=90°,∠BPC=45°,∠PBA=θ.
如图,B为△APC的边AC上的一点,且AB=BC=a,∠APB=90°,∠BPC=45°,∠PBA=θ. 的值.
的值. 的值.
的值.