Question

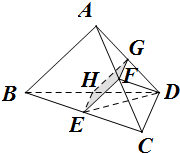已知四面体ABCD中，DC⊥BD，AB=AD=2DC=2．AD⊥平面EFGH，且AB∥截面EFGH，CD∥截面EFGH．
（Ⅰ）求证：GF∥CD，AB∥GH；
（Ⅱ）求证：GF⊥平面ABD；
（Ⅲ）设GD=x，求四棱锥D-EFGH的体积V（x）的最大值．

Answer 1

分析：（Ⅰ）利用线面平行的性质证明GF∥CD，AB∥GH；
（Ⅱ）根据线面垂直的判定定理证明GF⊥平面ABD；
（Ⅲ）根据四棱锥的体积公式求体积，利用导数求体积的最大值．

解答：解：因为CD∥截面EFGH且CD?面ADC，面ADC∩面EFGH=GH，
所以GF∥CD，同理AB∥GH．
（Ⅱ）因为DC⊥BD，GF∥CD，所以AD⊥GF，
又BD∩AD=D，所以GF⊥面ABD．
（Ⅲ）由（Ⅰ）知GF∥CD，AB∥GH，
同（Ⅰ）的证明方法可得，AB∥EF，HE∥CD，
所以GH∥EF．HE∥GF，
所以EFGH是平行四边形．
又GF⊥面ABD，所以GF⊥GF，
所以EFGH是矩形．
在△ABD中，

GH

AB

=

GD

AD

，所以GH=GD=x，
在△ACD中，

GF

DC

=

AG

AD

，所以GF=

2-x

2

．
所以矩形EFGH的面积S=GH•GF=x•

2-x

2

，
因为AD⊥平面EFGH，所以GD是四棱锥D-EFGH的高，
所以四棱锥D-EFGH的体积为V(x)=

1

3

GD?S=

1

3

x?x?

2-x

2

=

1

6

(-x3+2x2)，x∈(0，2)．
则V′(x)=

1

6

(-3x2+4x)，令V'（x）=0，得x=0（舍去）或x=

4

3

．
当0＜x＜

4

3

时，V'（x）＞0，此时V（x）在（0，

4

3

）上单调递增．
当

4

3

＜x＜2时，V'（x）＜0，此时V（x）在（

4

3

，2）上单调递减．
所以四棱锥D-EFGH的体积V（x）的最大值为V(

4

3

)=

1

6

(-

64

27

+2×

16

9

)=

16

81

．

点评：本题主要考查直线平行和直线与平面垂直的判断和应用，考查学生分析问题的能力．