题目内容

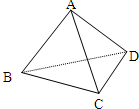已知四面体ABCD中，BD=
3
，BC=DC=1，其余棱长均为2，且四面体ABCD的顶点A、B、C、D都在同一个球面上，则这个球的表面积是（　　）
分析：由已知中四面体ABCD中，已知，BD=
3
，BC=DC=1，其余棱长均为2，我们设A在底面BCD上的射影为E，球的球心为O，利用解直角三角形，求出四面体ABCD外接球的半径，代入球的表面积公式，即可求出四面体ABCD外接球的面积．
解答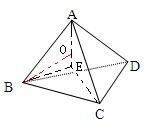：解：设A在底面BCD上的射影为E，球的球心为O，如图．
由正弦定理得：2BE=
BD
sin∠BCD
=
3
sin120°
=2，
∴BE=1，
在直角三角形ABE中，AE=
AB 2-BE 2
=
4-1
=
3
，
设OA=OB=R，在直角三角形BEO中，OB2=OE2+BE2，
即R2=12+（
3
-R）2，
∴R=
2
3

则这个球的表面积是4πR2=
16π
3
，
故选D．
点评：本题考查的知识点是棱锥的体积和球的表面积，其中计算外接球的半径，确定棱锥的高是关键，而求三棱锥的外接球表面积时，最难的问题是求外接球的半径．
练习册系列答案
相关题目
已知四面体ABCD中，AB=2，CD=1，AB与CD间的距离与夹角分别为3与30°，则四面体ABCD的体积为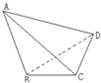（　　）精英家教网
A、
1
2
B、1
C、2
D、
3
2
精英家教网已知四面体ABCD中，DA=DB=DC=3
2
，且DA，DB，DC两两互相垂直，点O是△ABC的中心，将△DAO绕直线DO旋转一周，则在旋转过程中，直线DA与直线BC所成角的余弦值的取值范围是
 
．
 已知四面体ABCD中，DA=DB=DC=3
2
，且DA，DB，DC两两互相垂直，点O是△ABC的中心，将△DAO绕直线DO旋转一周，则在旋转过程中，直线DA与直线BC所成角的余弦值的最大值是
6
3
6
3
．
已知四面体ABCD中，AB=AD=6，AC=4，CD=2
13
，AB⊥平面ACD，则四面体ABCD外接球的表面积为（　　）
A、36πB、88π
C、92πD、128π

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

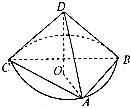精英家教网