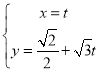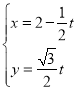题目内容
【题目】已知数列![]() 中,
中, 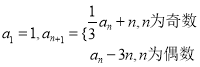 .
.
(1)求证:数列![]() 是等比数列;
是等比数列;
(2)若是![]() 数列
数列![]() 的前
的前![]() 项和,求满足
项和,求满足![]() 的所有正整数
的所有正整数![]() .
.
【答案】(1)见解析;(2)1和2.
【解析】试题分析:(1)要证明数列![]() 是等比数列,只需根据等比数列的定义,为此设
是等比数列,只需根据等比数列的定义,为此设![]() ,因此证明
,因此证明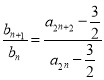 为常数即可;(2)首先要求
为常数即可;(2)首先要求![]() 的通项,由(1)可得出
的通项,由(1)可得出![]() ,即
,即![]() ,则递推式可得
,则递推式可得![]() ,由于通项
,由于通项![]() 要分类,因此求数列的和时,我们也分类讲解,
要分类,因此求数列的和时,我们也分类讲解, 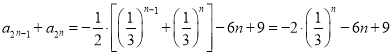 ,
,
![]() ,这是递减的,计算发现
,这是递减的,计算发现![]() ,又
,又![]() ,同理可得
,同理可得![]() ,即满足题意的
,即满足题意的![]() 只有1和2两个数.
只有1和2两个数.
试题解析:(Ⅰ)设![]() ,
,
因为
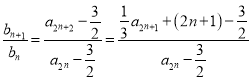 =
=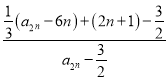 =
=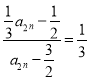 ,
,
所以数列![]() 是以
是以![]() 即
即![]() 为首项,以
为首项,以![]() 为公比的等比数列. 5分
为公比的等比数列. 5分
(Ⅱ)由(Ⅰ)得![]() ,即
,即![]() ,
,
由![]() ,得
,得![]() ,
,
所以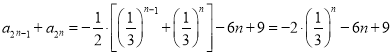 ,
,
![]()
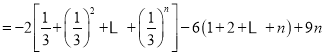
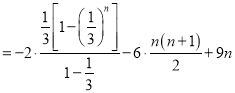
![]() .10分
.10分
显然当![]() 时,
时, ![]() 单调递减,
单调递减,
又当![]() 时,
时, ![]() >0,当
>0,当![]() 时,
时, ![]() <0,所以当
<0,所以当![]() 时,
时, ![]() <0;
<0;
![]() ,
,
同理,当且仅当![]() 时,
时, ![]() >0,
>0,
综上,满足![]() 的所有正整数
的所有正整数![]() 为1和2. 13分
为1和2. 13分

练习册系列答案
相关题目