题目内容
某同学参加某高校的自主招生考试(该测试只考语文、数学、英语三门课程),其中该同学语文取得优秀成绩的概率为0.5,数学和英语取得优秀成绩的概率分别为p,q(p<q),且不同课程取得优秀成绩相互独立.记ξ为该生取得优秀成绩的课程数,其分布列为:| ξ | 1 | 2 | 3 | |
| P | 0.12 | a | b | 0.12 |
(2)求数学期望Eξ
【答案】分析:(1)用A表示“该生语文课程取得优秀成绩”,用B表示“该生数学课程取得优秀成绩”,用C表示“该生英语课程取得优秀成绩”,由题意得P(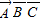 )=(1-0.5)(1-p)(1-q)=0.12,P(ABC)=0.5pq=0.12,由此能求出p,q.
)=(1-0.5)(1-p)(1-q)=0.12,P(ABC)=0.5pq=0.12,由此能求出p,q.
(2)由题设知ξ的可能取值为0,1,2,3,分别求出其概率,由此能够求出数学期望Eξ.
解答:解:(1)用A表示“该生语文课程取得优秀成绩”,
用B表示“该生数学课程取得优秀成绩”,
用C表示“该生英语课程取得优秀成绩”,
由题意得P(A)=0.5,P(B)=p,P(C)=q,p<q,
P(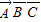 )=(1-0.5)(1-p)(1-q)=0.12,
)=(1-0.5)(1-p)(1-q)=0.12,
P(ABC)=0.5pq=0.12,
解得p=0.4,q=0.6.
(2)由题设知ξ的可能取值为0,1,2,3,
P(ξ=0)=0.12,
P(ξ=1)=P(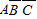 )+P(
)+P(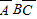 )+P(
)+P(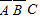 )
)
=0.5×(1-0.4)×(1-0.6)+(1-0.5)×0.4×(1-0.6)+(1-0.5)×(1-0.4)×0.6
=0.38,
P(ξ=2)=P(AB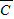 )+P(A
)+P(A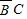 )+P(
)+P(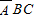 )
)
=0.5×0.4×(1-0.6)+0.5×(1-0.4)×0.6+(1-0.5)×0.4×0.6
=0.38,
P(ξ=3)=0.12,
∴Eξ=0×0.12+1×0.38+2×0.38+3×0.12=1.5.
点评:本题考查离散随机变量的概率分布列和数学期望,是历年高考的必考题型之一.解题时要认真审题,注意排列组合知识和概率知识的灵活运用.
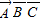 )=(1-0.5)(1-p)(1-q)=0.12,P(ABC)=0.5pq=0.12,由此能求出p,q.
)=(1-0.5)(1-p)(1-q)=0.12,P(ABC)=0.5pq=0.12,由此能求出p,q.(2)由题设知ξ的可能取值为0,1,2,3,分别求出其概率,由此能够求出数学期望Eξ.
解答:解:(1)用A表示“该生语文课程取得优秀成绩”,
用B表示“该生数学课程取得优秀成绩”,
用C表示“该生英语课程取得优秀成绩”,
由题意得P(A)=0.5,P(B)=p,P(C)=q,p<q,
P(
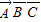 )=(1-0.5)(1-p)(1-q)=0.12,
)=(1-0.5)(1-p)(1-q)=0.12,P(ABC)=0.5pq=0.12,
解得p=0.4,q=0.6.
(2)由题设知ξ的可能取值为0,1,2,3,
P(ξ=0)=0.12,
P(ξ=1)=P(
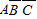 )+P(
)+P(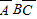 )+P(
)+P(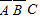 )
)=0.5×(1-0.4)×(1-0.6)+(1-0.5)×0.4×(1-0.6)+(1-0.5)×(1-0.4)×0.6
=0.38,
P(ξ=2)=P(AB
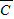 )+P(A
)+P(A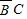 )+P(
)+P(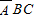 )
)=0.5×0.4×(1-0.6)+0.5×(1-0.4)×0.6+(1-0.5)×0.4×0.6
=0.38,
P(ξ=3)=0.12,
∴Eξ=0×0.12+1×0.38+2×0.38+3×0.12=1.5.
点评:本题考查离散随机变量的概率分布列和数学期望,是历年高考的必考题型之一.解题时要认真审题,注意排列组合知识和概率知识的灵活运用.

练习册系列答案
相关题目
 、
、 ,两题全部答对方可进入面试。面试要回答甲、乙两个问题,该学生答对这两个问题的概率均为
,两题全部答对方可进入面试。面试要回答甲、乙两个问题,该学生答对这两个问题的概率均为 ,两题全部答对方可进入面试.面试要回答甲、乙两个问题,该学生答对两个问题的概率均为
,两题全部答对方可进入面试.面试要回答甲、乙两个问题,该学生答对两个问题的概率均为 ,至少答对一题即可被录取.(假设每个环节的每个问题回答正确与否是相对独立的).
,至少答对一题即可被录取.(假设每个环节的每个问题回答正确与否是相对独立的). ,两题全部答对方可进入面试.面试要回答甲、乙两个问题,该学生答对两个问题的概率均为
,两题全部答对方可进入面试.面试要回答甲、乙两个问题,该学生答对两个问题的概率均为 ,至少答对一题即可被录取.(假设每个环节的每个问题回答正确与否是相对独立的).
,至少答对一题即可被录取.(假设每个环节的每个问题回答正确与否是相对独立的).