题目内容
为了在夏季降温和冬季供暖时减少能源损耗,房屋的屋顶和外墙需要建造隔热层.某幢建筑物要建造可使用20年的隔热层,每厘米厚的隔热层建造成本为6万元.该建筑物每年的能源消耗费用C(单位:万元)与隔热层厚度x(单位:cm)满足关系:C(x)= ,若不建隔热层(即x=0时),每年能源消耗费用为8万元.设f(x)为隔热层建造费用与20年的能源消耗费用之和.
,若不建隔热层(即x=0时),每年能源消耗费用为8万元.设f(x)为隔热层建造费用与20年的能源消耗费用之和.
(1)求k的值;
(2)求f(x)的表达式;
(3)利用“函数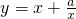 (其中a为大于0的常数),在
(其中a为大于0的常数),在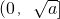 上是减函数,在
上是减函数,在 上是增函数”这一性质,求隔热层修建多厚时,总费用f(x)达到最小,并求出这个最小值.
上是增函数”这一性质,求隔热层修建多厚时,总费用f(x)达到最小,并求出这个最小值.
解:(1)根据题意当x=0时,C(x)=8,代入得 =8?K=40;
=8?K=40;
(2)f(x)=6x+20× =6x+
=6x+ ,0≤x≤10.
,0≤x≤10.
(3)∵f(x)=2(3x+5)+ -10=2[(3x+5)+
-10=2[(3x+5)+ ]-10≥2×2
]-10≥2×2 -10=70.
-10=70.
当且仅当3x+5= =20时,即x=5时,取“=”.
=20时,即x=5时,取“=”.
答:隔热层修建5厘米厚时,总费用最小,最小值为70(万元).
分析:(1)根据题意中的一组特值求解.
(2)根据题意,隔热层的建造费用f(x)是20年的能源消耗费用之和与x厘米厚的隔热层的建造成本的和,依次求出函数的解析式与定义域.
(3)将函数解析式化简,再利用“函数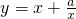 (其中a为大于0的常数),在
(其中a为大于0的常数),在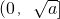 上是减函数,在
上是减函数,在 上是增函数”这一性质,求解.
上是增函数”这一性质,求解.
点评:本题主要考查利用构造函数类型解决实际问题.
 =8?K=40;
=8?K=40;(2)f(x)=6x+20×
 =6x+
=6x+ ,0≤x≤10.
,0≤x≤10.(3)∵f(x)=2(3x+5)+
 -10=2[(3x+5)+
-10=2[(3x+5)+ ]-10≥2×2
]-10≥2×2 -10=70.
-10=70.当且仅当3x+5=
 =20时,即x=5时,取“=”.
=20时,即x=5时,取“=”.答:隔热层修建5厘米厚时,总费用最小,最小值为70(万元).
分析:(1)根据题意中的一组特值求解.
(2)根据题意,隔热层的建造费用f(x)是20年的能源消耗费用之和与x厘米厚的隔热层的建造成本的和,依次求出函数的解析式与定义域.
(3)将函数解析式化简,再利用“函数
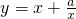 (其中a为大于0的常数),在
(其中a为大于0的常数),在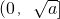 上是减函数,在
上是减函数,在 上是增函数”这一性质,求解.
上是增函数”这一性质,求解.点评:本题主要考查利用构造函数类型解决实际问题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目