题目内容
19．函数f（x）=x2-4x-2lnx+5的零点个数为（ ）| A． | 3 | B． | 2 | C． | 1 | D． | 0 |
分析 函数f（x）=x2-4x-2lnx+5的零点个数即函数y=x2-4x+5与函数y=2lnx的交点的个数，作函数y=x2-4x+5与函数y=2lnx的图象，结合图象求解．
解答 解：函数f（x）=x2-4x-2lnx+5的零点个数即函数y=x2-4x+5与函数y=2lnx的交点的个数，
作函数y=x2-4x+5与函数y=2lnx的图象如下，
结合图象可得，
函数f（x）=x2-4x-2lnx+5的零点个数为2；
故选：B．
点评 本题考查了函数的零点与函数的图象的交点的应用，属于基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
9．某几何体的三视图如图所示，且该几何体的所有棱中，则该几何体的所有棱中，最长的棱为（ ）
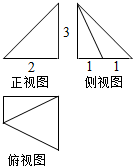
| A． | $\sqrt{14}$ | B． | $\sqrt{13}$ | C． | $\sqrt{5}$ | D． | 4 |
10．微信是现代生活进行信息交流的重要工具，距据统计，某公司200名员工中90%的人使用微信，其中每天使用微信时间在一小时以内的有60人，其余每天使用微信在一小时以上，若将员工年龄分成青年（年龄小于40岁）和中年（年龄不小于40岁）两个阶段，使用微信的人中75%是青年人，若规定：每天使用微信时间在一小时以上为经常使用微信，经常使用微信的员工中$\frac{2}{3}$是青年人．
（Ⅰ）若要调查该公司使用微信的员工经常使用微信与年龄的关系，列出2×2列联表．
2×2列联表．
（Ⅱ）由列联表中所得数据，是否有99.9%的把握认为“经常使用微信与年龄有关”？
（Ⅲ）采用分层抽样的方法从“经常使用微信”中抽取6人，从这6人中任选2人，求事件A“选出的2人均是青年人”的概率．
附：
K2=$\frac{n（ad-bc）^{2}}{（a+b）（c+d）（a+c）（b+d）}$．
（Ⅰ）若要调查该公司使用微信的员工经常使用微信与年龄的关系，列出2×2列联表．
2×2列联表．
| 青年人 | 中年人 | 合计 | |
| 经常使用微信 | |||
| 不经常使用微信 | |||
| 合计 |
（Ⅲ）采用分层抽样的方法从“经常使用微信”中抽取6人，从这6人中任选2人，求事件A“选出的2人均是青年人”的概率．
附：
| P（K2≥k） | 0.010 | 0.001 |
| k | 6.635 | 10.828 |
如图，已知椭圆：$\frac{{x}^{2}}{4}$+y2=1，点A，B是它的两个顶点，过原点且斜率为k的直线l与线段AB相交于点D，且与椭圆相交于E、F两点．