题目内容
已知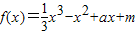
，其中a＞0，如果存在实数t，使f'（t）＜0，则
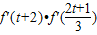的值（ ）A．必为正数
B．必为负数
C．必为非负
D．必为非正
【答案】分析：先对f（x）求导，由已知条件a＞0，如果存在实数t，使f'（t）＜0，求出t与a的取值范围，进而比较出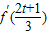
、f′（t+2）与0的关系，从而得出答案．
解答：解：∵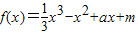
，∴f′（x）=x2-2x+a．
∵存在实数t，使f'（t）＜0，a＞0，∴t2-2t+a＜0的解集不是空集，
∴△=4-4a＞0，解得a＜1，因此0＜a＜1．
令t2-2t+a=0，解得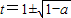
，
∴t2-2t+a＜0的解集是{x|0＜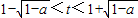
＜2}．
∵f′（t+2）=（t+2）2-2（t+2）+a=t（t+2）+a，∴f′（t+2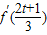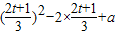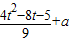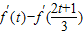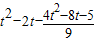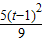）＞0；
∵
=
=
，
∴
=
=
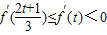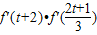≥0，
∴
，
∴
＜0，
故选B．
点评：由已知得出a与t的取值范围和利用作差法比较两个数的大小是解题的关键．
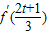、f′（t+2）与0的关系，从而得出答案．解答：解：∵
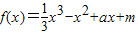，∴f′（x）=x2-2x+a．∵存在实数t，使f'（t）＜0，a＞0，∴t2-2t+a＜0的解集不是空集，
∴△=4-4a＞0，解得a＜1，因此0＜a＜1．
令t2-2t+a=0，解得
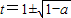，∴t2-2t+a＜0的解集是{x|0＜
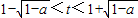＜2}．∵f′（t+2）=（t+2）2-2（t+2）+a=t（t+2）+a，∴f′（t+2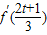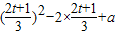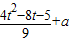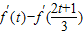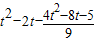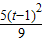）＞0；
∵
==，∴
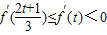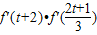==≥0，∴
，∴
＜0，故选B．
点评：由已知得出a与t的取值范围和利用作差法比较两个数的大小是解题的关键．
练习册系列答案
举一反三同步巧讲精练系列答案
口算与应用题卡系列答案
相关题目
已知函数f（x）=Asin（ωx+φ）（其中
(其中A＞0，ω＞0，
)的图象如图所示．
的值；
的值．
(其中A>0,
)的图象如图所示.
,求
的值.
=a,
=b,而M、N分别是△AOB的两边OA、OB上的点,且
=λa(0＜λ＜1),
=μb(0＜μ＜1),设BM与AN相交于P,试将向量
=p用a、b表示出来.
(其中A>0,
)的图象如图所示。
,求
的值。