题目内容
如图2-4所示,已知△AOB,其中
图2-4
解:由题图可知p=![]() 或p=
或p=![]() ,而
,而![]() =λa,
=λa,
设![]() =m(
=m(![]() )=m(b-λa),
)=m(b-λa),
又∵![]() =μb,设
=μb,设![]() =n(
=n(![]() )=n(a-μb),
)=n(a-μb),
∴p=![]() =λa+m(b-λa)=λ(1-m)a+mb,
=λa+m(b-λa)=λ(1-m)a+mb,
p=![]() =μb+n(a-μb)=na+μ(1-n)b.
=μb+n(a-μb)=na+μ(1-n)b.
∵a、b不共线,且表示方法唯一,
∴![]() 解得
解得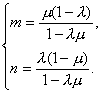
∴p=λ[![]() ]a+
]a+![]() ,
,
即p=![]() .
.

练习册系列答案
相关题目
题目内容
如图2-4所示,已知△AOB,其中
图2-4
解:由题图可知p=![]() 或p=
或p=![]() ,而
,而![]() =λa,
=λa,
设![]() =m(
=m(![]() )=m(b-λa),
)=m(b-λa),
又∵![]() =μb,设
=μb,设![]() =n(
=n(![]() )=n(a-μb),
)=n(a-μb),
∴p=![]() =λa+m(b-λa)=λ(1-m)a+mb,
=λa+m(b-λa)=λ(1-m)a+mb,
p=![]() =μb+n(a-μb)=na+μ(1-n)b.
=μb+n(a-μb)=na+μ(1-n)b.
∵a、b不共线,且表示方法唯一,
∴![]() 解得
解得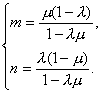
∴p=λ[![]() ]a+
]a+![]() ,
,
即p=![]() .
.
