题目内容
下列双曲线，离心率
的是（ ）
A． | B． |
C． | D． |
B
解析试题分析：四个选项依次验证离心率的值，找到相应的方程
考点：双曲线的几何性质：离心率
点评：由方程求离心率首先找到a,c的值
练习册系列答案
阅读快车系列答案
相关题目
已知抛物线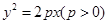
的焦点为
，点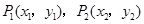
，
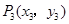在抛物线上，且
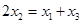， 则有 （ ）
A． | B． |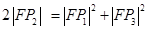
C． | D． |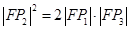
双曲线
的离心率为
，则它的渐近线方程为
A． | B． | C． | D． |
已知椭圆
=1双曲线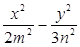
＝1有公共的焦点，那么双曲线的渐近线方程是（ ）
A．x＝± | B．y＝± | C．x＝± | D．y＝± |
过
的焦点
作直线交抛物线与
两点，若
与
的长分别是
，则
（ ）
A． | B． | C． | D． |
已知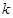
＜4,则曲线
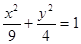和
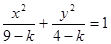有 ( )
| A．相同的准线 | B．相同的焦点 |
| C．相同的离心率 | D．相同的长轴 |
过双曲线的右焦点F作实轴所在直线的垂线，交双曲线于A，B两点，设双曲线的左顶点M，若点M在以AB为直径的圆的内部，则此双曲线的离心率e的取值范围为( )
A．( ，+∞) | B．(1，) | C．(2，+∞) | D．(1，2) |
抛物线
的焦点到准线的距离是（ ）
A． | B． | C． | D． |