题目内容
(本题满分12分)
已知数列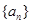 为公差不为
为公差不为 的等差数列,
的等差数列,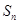 为前
为前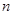 项和,
项和,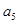 和
和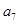 的等差中项为
的等差中项为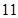 ,且
,且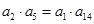 .令
.令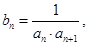 数列
数列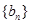 的前
的前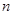 项和为
项和为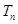 .
.
(Ⅰ)求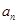 及
及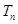 ;
;
(Ⅱ)是否存在正整数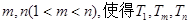 成等比数列?若存在,求出所有的
成等比数列?若存在,求出所有的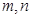 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(Ⅰ) ,
, 
(Ⅱ)当 可以使
可以使 成等比数列.
成等比数列.
解析
试题分析:(Ⅰ)因为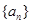 为等差数列,设公差为
为等差数列,设公差为 ,则由题意得
,则由题意得
整理得
所以 ……………3分
……………3分
由
所以 ……………5分
……………5分
(Ⅱ)假设存在
由(Ⅰ)知, ,所以
,所以
若 成等比,则有
成等比,则有 ………8分
………8分 ,。。。。。(1)
,。。。。。(1)
因为 ,所以
,所以 ,……………10分
,……………10分
因为 ,当
,当 时,带入(1)式,得
时,带入(1)式,得 ;
;
综上,当 可以使
可以使 成等比数列.……………12分
成等比数列.……………12分
考点:本题考查了数列的通项公式及前N项和的求法
点评:高考中中的数列解答题考查的的热点为求数列的通项公式、等差(比)数列的性质及数列的求和问题.因此在高考复习的后期,要特别注意加强对由递推公式求通项公式、求有规律的非等差(比)数列的前n项和等的专项训练.

练习册系列答案
相关题目
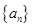 满足
满足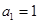 ,
,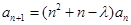 (
(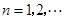 ),
),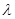 是常数.
是常数.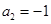 时,求
时,求 的值;
的值; 具有性质:①
具有性质:① 为整数;②对于任意的正整数
为整数;②对于任意的正整数 ,当
,当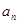 为偶数时,
为偶数时, ;当
;当 .
. 成等差数列,求
成等差数列,求 (
( 且
且 N),数列
N),数列 ,求证:
,求证: ;
; (
( N)时,都有
N)时,都有 .
. :
: 上的点
上的点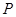 到点
到点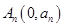 的距离的最小值为
的距离的最小值为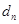 ,若
,若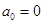 ,
,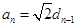 ,
,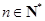
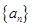 的通项公式;
的通项公式; ;
;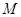 ,使得对
,使得对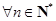 ,都有不等式:
,都有不等式: 成立?请说明理由.
成立?请说明理由. 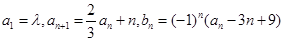 ,其中λ为实数,n为正整数.
,其中λ为实数,n为正整数.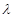 的值;
的值; tan x+1=0在x
tan x+1=0在x [0,n
[0,n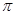 )( n
)( n bn,求实数k的取值范围.
bn,求实数k的取值范围.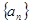 中,
中, 为常数,
为常数,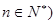 ,且
,且 成公比不等于1的等比数列.
成公比不等于1的等比数列. 的值;
的值; ,求数列
,求数列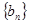 的前
的前 项和
项和 。
。 的前n项和
的前n项和 ,且
,且 是
是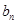 与1的等差中项。
与1的等差中项。 的通项公式;
的通项公式; ,求
,求
 ,是否存在
,是否存在 ,使得
,使得 并说明理由。
并说明理由。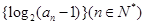 为等差数列,且
为等差数列,且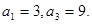
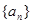 的通项公式;
的通项公式;