题目内容
想象一下一个人从出生到死亡,在每个生日都测量身高,并作出这些数据的散点图,这些点将不会落在一条直线上,但在一段时间内的增长数据有时可以用线性回归来分析,下表是一位母亲给儿子做的成长记录:
(1)年龄(解释变量)和身高(预报变量)之间具有怎样的相关关系?
(2)如果年龄相差5岁,则身高有多大差异(3~16岁之间)?
(3)如果身高相差20 cm,其年龄相差多少(3~16岁之间)?
(4)计算残差,说明该函数模型是否能够较好地反映年龄与身高的关系,说明理由.
| 年龄/周岁 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 身高/cm | 91.8 | 97.6 | 104.2 | 110.9 | 115.6 | 122.0 | 128.5 |
| | |||||||
| 年龄/周岁 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| 身高/cm | 134.2 | 140.8 | 147.6 | 154.2 | 160.9 | 167.5 | 173.0 |
(2)如果年龄相差5岁,则身高有多大差异(3~16岁之间)?
(3)如果身高相差20 cm,其年龄相差多少(3~16岁之间)?
(4)计算残差,说明该函数模型是否能够较好地反映年龄与身高的关系,说明理由.
(1) =6.286x+72 (2) 31.4 cm (3) 3(岁) (4) 拟合效果较好
=6.286x+72 (2) 31.4 cm (3) 3(岁) (4) 拟合效果较好
 =6.286x+72 (2) 31.4 cm (3) 3(岁) (4) 拟合效果较好
=6.286x+72 (2) 31.4 cm (3) 3(岁) (4) 拟合效果较好解:(1)设年龄x与身高y之间的回归直线方程为
 =
= x+
x+ ,由公式
,由公式 =
= 得
得 ≈6.286,
≈6.286, =
= -
-
 ≈72,所以
≈72,所以 =6.286x+72.
=6.286x+72.(2)如果年龄相差5岁,则预报变量变化6.286×5=31.425,即身高相差约31.4 cm.
(3)如果身高相差20 cm,年龄相差Δx=
 =3.182≈3(岁).
=3.182≈3(岁).(4)
| y | 91.8 | 97.6 | 104.2 | 110.9 | 115.6 | 122.0 | 128.5 |
 i i | 90.9 | 97.1 | 103.4 | 109.7 | 116.0 | 122.3 | 128.6 |
| | |||||||
| y | 134.2 | 140.8 | 147.6 | 154.2 | 160.9 | 167.5 | 173.0 |
 i i | 134.9 | 141.1 | 147.4 | 153.7 | 160.0 | 166.3 | 172.6 |
 ≈0.999 7.由R2=0.999 7,表明年龄解释了99.97%的身高的变化,拟合效果较好.
≈0.999 7.由R2=0.999 7,表明年龄解释了99.97%的身高的变化,拟合效果较好.
练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
 小于
小于 为二等品,小于
为二等品,小于 元,生产一件三等品亏损10元.现随机抽查熟练工人甲和新工人乙生产的这种产品各100件进行检测,检测结果统计如下:
元,生产一件三等品亏损10元.现随机抽查熟练工人甲和新工人乙生产的这种产品各100件进行检测,检测结果统计如下:






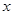 表示.
表示.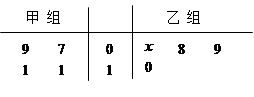
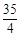 ,求
,求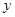 (吨)与气温
(吨)与气温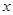 (℃)之间的关系,随机统计并制作了5天该小区居民用水量与当天气温的对应表:
(℃)之间的关系,随机统计并制作了5天该小区居民用水量与当天气温的对应表: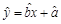 中的
中的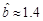 ,试求出
,试求出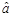 的值,并预测当地气温为5℃时,该生活小区的用水量.
的值,并预测当地气温为5℃时,该生活小区的用水量.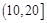 ,2;
,2;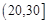 ,3;
,3; ,4;
,4; ,5;
,5; ,4;
,4;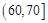 ,2.则样本在
,2.则样本在 上的频率是 .
上的频率是 .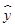 =
=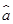 +
+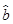 x,关于回归系数
x,关于回归系数 ,则有( )
,则有( )




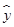 =0.30x+9.99.根据建设项目的需要,28天后混凝土的抗压度不得低于89.7 kg/cm2,每立方米混凝土的水泥用量最少应为________kg.(精确到0.1 kg)
=0.30x+9.99.根据建设项目的需要,28天后混凝土的抗压度不得低于89.7 kg/cm2,每立方米混凝土的水泥用量最少应为________kg.(精确到0.1 kg)