题目内容
设(x1,y1)，(x2,y2)，…，(xn,yn)，是变量x:和y的n个样本点，直线Z是由这些样本点通过 最小二乘法得到的线性回归方程(如图），以下结论中正确的是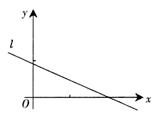
| A．x;和y正相关 |
| B．y和y的相关系数为直线I的斜率 |
| C．x和y的相关系数在-1到O之间 |
| D．当n为偶数时，分布在l两侧的样本点的个数一定相同 |
C
解析试题分析：
考点：本试题考查了散点图的知识点。
点评：解决该试题的关键是能利用直线的变化规律：由左下方到右上方，说明是正相关，由左上方到右下方为负相关。因此可知选项A错误。那么相关系数不是表示的为直线的斜率，因此B错误，同时对于选项D，点的分布位置，在直线的两侧的点的个数不一定相同，因此错误，而选项 C中，可知x和y的相关系数在-1到O之间，显然符合概念，故选C.
已知一组正数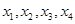
的方差为
，则数据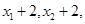
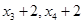的平均数为( )
| A．2 | B．4 | C．-2 | D．不确定 |
在独立性检验中，统计量
有两个临界值：3.841和6.635；当＞3.841时，有95%的把握说明两个事件有关，当＞6.635时，有99%的把握说明两个事件有关，当
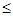3.841时，认为两个事件无关.在一项打鼾与患心脏病的调查中，共调查了2000人，经计算的=20.87，根据这一数据分析，认为打鼾与患心脏病之间
| A．有95%的把握认为两者有关 | B．约有95%的打鼾者患心脏病 |
| C．有99%的把握认为两者有关 | D．约有99%的打鼾者患心脏病 |
某初级中学采用系统抽样方法，从该校全体800名学生中抽50名做健康检查．现将800名学生从1到800进行编号，求得间隔数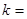
＝16，即每16人抽取一个人．在1~16中随机抽取一个数，如果抽到的是7，则从33 ~ 48这16个数中应取的数是
| A．40 | B．39 | C．38 | D．37 |
将参加夏令营的600名学生编号为：001,002，…，600.采用系统抽样方法抽取一个容量为50的样本，且随机抽得的号码为003.这600名学生分住在三个营区，从001到300在第Ⅰ营区，从301到495在第Ⅱ营区，从496到600在第Ⅲ营区，三个营区被抽中的人数依次为( )
| A．26,16,8 | B．25,17,8 | C．25,16,9 | D．24,17,9 |
从四个公司按分层抽样的方法抽取职工参加知识竞赛，其中甲公司共有职工96人．若从甲、乙、丙、丁四个公司抽取的职工人数分别为12，21，25，43，则这四个公司的总人数为
| A．101 | B．808 | C．1212 | D．2012 |
已知某产品的广告费用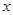
万元与销售额
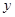万元的统计数据如表所示：
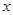| （万元） | 0 | 1 | 3 | 4 |
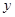| （万元） | 2.2 | 4.3 | 4.8 | 6.7 |
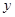与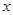线性相关，且
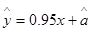，则据此模型预报广告费用为6万元时销售额为A. 2.6万元 B. 8.3万元 C. 7.3万元 D. 9.3万元
某产品的广告费用x与销售额y的统计数据如下表：
| 广告费用x（万元） | 4 | 2 | 3 | 5 |
| 销售额y（万元） | 49 | 26 | 39 | 54 |
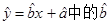为9.4，据此预报广告费用为6万元时销售额约为（ ）A、63.6万元 B、65.5万元 C、67.7万元 D、72.0万元
一个年级有12个班，每个班有50名学生，随机编为1～50号，为了解他们在课外的兴趣爱好。要求每班是40号学生留下来进行问卷调查，这里运用的抽样方法是（ ）
| A．分层抽样 | B．抽签法 | C．随机数表法 | D．系统抽样法 |