题目内容
已知一组正数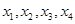 的方差为
的方差为 ,则数据
,则数据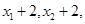
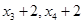 的平均数为( )
的平均数为( )
| A.2 | B.4 | C.-2 | D.不确定 |
B
解析试题分析:设正数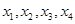 的平均数为
的平均数为 ,由方差的计算公式得,
,由方差的计算公式得, ,所以
,所以 。
。 =2,故
=2,故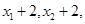
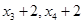 的平均数为4,选B。
的平均数为4,选B。
考点:本题主要考查方差和平均数的性质。
点评:简单题,一般地设有n个数据,x1,x2,…xn,若每个数据都放大或缩小相同的倍数后再同加或同减去一个数,其平均数也有相对应的变化,方差则变为这个倍数的平方倍。

练习册系列答案
相关题目
已知某单位有职工120人,其中男职工90人。现在采用分层抽样(按男女分层)抽取一个样本,若样本中有3名女职工,则样本容量为( )。
| A.9 | B.12 | C.10 | D.15 |
某产品的广告费用 与销售额
与销售额 的统计数据如下表:
的统计数据如下表:
广告费用 (万元) (万元) | 4 | 2 | 3 | 5 |
销售额 (万元) (万元) | 49 | 26 | 39 | 54 |
 中的
中的 为
为 ,据此模型预报广告费用为
,据此模型预报广告费用为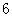 万元时销售额为( )
万元时销售额为( )A、
 万元 B、
万元 B、 万元
万元 C、
 万元 D、
万元 D、 万元
万元 已知回归直线的斜率的估计值是1.23,样本点的中心为(4,5),则回归直线的方程是( )
A. =1.23x+4 =1.23x+4 | B. =1.23x+5 =1.23x+5 | C. =1.23x+0.08 =1.23x+0.08 | D. =0.08x+1.23 =0.08x+1.23 |
某苗圃基地为了解基地内甲、乙两块地种植的同一种树苗的长势情况,从两块地各随机抽取了10株树苗,用茎叶图表示上述两组数据,对两块地抽取树苗的高度的平均数 、
、 和中位数
和中位数 进行比较,下面结论正确的是
进行比较,下面结论正确的是

A. | B. |
C. | D. |
设(x1,y1),(x2,y2),…,(xn,yn),是变量x:和y的n个样本点,直线Z是由这些样本点通过 最小二乘法得到的线性回归方程(如图),以下结论中正确的是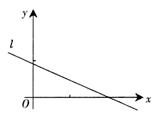
| A.x;和y正相关 |
| B.y和y的相关系数为直线I的斜率 |
| C.x和y的相关系数在-1到O之间 |
| D.当n为偶数时,分布在l两侧的样本点的个数一定相同 |
 )负相关,则其回归方程可能是( )
)负相关,则其回归方程可能是( ) B.
B. C.
C.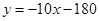 D
D 
 ,则变量
,则变量 增加一个单位时
增加一个单位时 减少
减少 个单位 B
个单位 B 个单位
个单位 =bx+a必过( )
=bx+a必过( ) B.点
B.点 C.点
C.点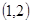 D.点
D.点