题目内容
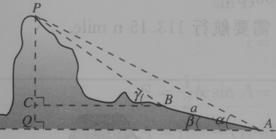
 如图:在山脚A测得山顶P的仰角为α=30°,沿倾斜角为β=15°的斜坡向上走10米到B,在B处测得山顶P的仰角为γ=60°,求山高h(单位:米)
如图:在山脚A测得山顶P的仰角为α=30°,沿倾斜角为β=15°的斜坡向上走10米到B,在B处测得山顶P的仰角为γ=60°,求山高h(单位:米)分析:△PAB中,∠PAB=α-β=15°,∠BPA=(
-α)-(
-γ)=γ-α=30°,由正弦定理可求PB,根据PQ=PC+CQ=PB•sinγ+asinβ 可得结果.
| π |
| 2 |
| π |
| 2 |
解答:解:△PAB中,∠PAB=α-β=15°,∠BPA=(
-α)-(
-γ)=γ-α=30°,
∴
=
,∴PB=5(
-
).
∴PQ=PC+CQ=PB•sinγ+10sinβ=5(
-
)×sin60°+10sin15°=5
米
即山高为5
米
| π |
| 2 |
| π |
| 2 |
∴
| 10 |
| sin30° |
| PB |
| sin15° |
| 6 |
| 2 |
∴PQ=PC+CQ=PB•sinγ+10sinβ=5(
| 6 |
| 2 |
| 2 |
即山高为5
| 2 |
点评:本题考查正弦定理的应用,直角三角形中的边角关系,求出PB是解题的关键.

练习册系列答案
相关题目
 如图:在山脚A测得山顶P的仰角为α=30°,沿倾斜角为β=15°的斜坡向上走10米到B,在B处测得山顶P的仰角为γ=60°,求山高h(单位:米)
如图:在山脚A测得山顶P的仰角为α=30°,沿倾斜角为β=15°的斜坡向上走10米到B,在B处测得山顶P的仰角为γ=60°,求山高h(单位:米)