题目内容
在四棱锥P-ABCD中，△PBC为正三角形，AB⊥平面PBC，AB∥CD，AB=
DC，
．F为PC中点。（1）求证：AE∥平面PBC；（2）求证：AE⊥平面PDC．
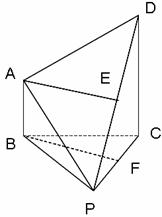
（1）证明:连接EF, ．F为PC中点,则EF∥CD，EF=DC, 因为AB∥CD，AB=DC，所以有EF∥AB且EF=AB,则四边形ABFE是平行四边形．所以AE∥BF,因为AE不在平面PBC内,BF在平面PBC内,所以AE∥平面PBC．（8分）
（2） 因为AB⊥平面PBC，AB∥CD,所以CD⊥平面PBC，BF在平面PBC内,CD⊥BF．
△PBC为正三角形,BF⊥PC,又PC
CD=C,PC、CD在平面PDC内，所以BF⊥平面PDC，又AE∥BF,所以AE⊥平面PDC． （14分）
练习册系列答案
相关题目
如图，在四棱锥P-ABCD中，底面为直角梯形，AD∥BC，∠BAD=90，PA⊥底面ABCD，且PA=AD=AB=2BC=2，M，N分别为PC、PB的中点．
如图，在四棱锥P-ABCD中，底面ABCD是矩形，PA⊥平面ABCD，PA=AD=4．AB=2，AN⊥PC于点N，M是PD中点．
如图，在四棱锥P-ABCD中，底面ABCD是矩形，O为底面中心，PA⊥平面ABCD，PA=AD=2AB．M是PD的中点
如图，在四棱锥P-ABCD中，底面ABCD是矩形，已知AB=3，AD=2，PA=2，PD=2
（2009•成都模拟）如图，在四棱锥P-ABCD中，底面ABCD为正方形，且PD⊥平面ABCD，PD=AB=1，EF分别是PB、AD的中点，