题目内容
1.要使式子$\sqrt{\frac{x-2}{x+2}}$有意义,则x的取值范围是( )| A. | x∈(-∞,-2)∪[2,+∞) | B. | x∈(-∞,-2]∪[2,+∞) | C. | x∈(-2,2) | D. | x∈[-2,2] |
分析 由根式内部的代数式大于等于0求解分式不等式得答案.
解答 解:要使$\sqrt{\frac{x-2}{x+2}}$有意义,则$\frac{x-2}{x+2}≥0$?$\left\{\begin{array}{l}{x+2≠0}\\{(x-2)(x+2)≥0}\end{array}\right.$,解得x<-2或x≥2.
∴x的取值范围是(-∞,-2)∪[2,+∞).
故选:A.
点评 本题考查函数的定义域及其求法,考查分式不等式的解法,是基础题.

练习册系列答案
相关题目
6.设a=log9$\sqrt{3}$,b=log3$\sqrt{\frac{8}{5}}$,c=$\frac{1}{6}$log23,则a,b,c之间的大小关系是( )
| A. | c>a>b | B. | a>c>b | C. | a>b>c | D. | c>b>a |
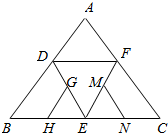 如图是正四面体的平面展开图,G、H、M、N分别为DE、BE、EF、EC的中点,在这个正四面体中,
如图是正四面体的平面展开图,G、H、M、N分别为DE、BE、EF、EC的中点,在这个正四面体中,