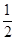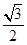题目内容
设等差数列 的前
的前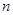 项和为
项和为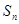 ,已知
,已知 ,
,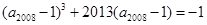 ,则下列结论中正确的是( )
,则下列结论中正确的是( )
A.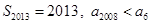 | B.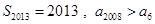 |
C.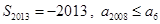 | D.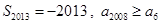 |
A
解析试题分析:先确定等差数列的公差d<0,再将条件相加,结合等差数列的求和公式及等差数列的性质,即可求得结论解:由 ,
,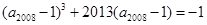 ,可得a6-1>0,-1<a2006-1<0,即a6>1,0<a2006<1,从而可得等差数列的公差d<0,∴a2016<a6,把已知的两式相加可得(a6-1)3+2012(a6-1)+(a2008-1)3+2012(a2008-1)=0整理可得(a6+a2008-2)•[(a6-1)2+(a2006-1)2-(a6-1)(a2006-1)+2013]=0,结合上面的判断可知(a6-1)2+(a2008-1)2-(a6-1)(a2008-1)+2012>0,所以a6+a2008=2,而
,可得a6-1>0,-1<a2006-1<0,即a6>1,0<a2006<1,从而可得等差数列的公差d<0,∴a2016<a6,把已知的两式相加可得(a6-1)3+2012(a6-1)+(a2008-1)3+2012(a2008-1)=0整理可得(a6+a2008-2)•[(a6-1)2+(a2006-1)2-(a6-1)(a2006-1)+2013]=0,结合上面的判断可知(a6-1)2+(a2008-1)2-(a6-1)(a2008-1)+2012>0,所以a6+a2008=2,而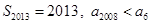 ,故选A.
,故选A.
考点:等差数列
点评:本题考查了等差数列的性质的运用,灵活利用等差数列的性质是解决问题的关键,属于中档题

练习册系列答案
相关题目
在数列 中,
中,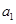 =1,
=1, ,则
,则 的值为 ( )
的值为 ( )
| A.99 | B.49 | C.102 | D.101 |
设等差数列 的前
的前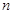 项和是
项和是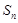 ,若
,若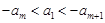 (
( N*,且
N*,且 ),则必定有( )
),则必定有( )
A. ,且 ,且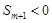 | B.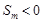 ,且 ,且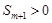 |
C. ,且 ,且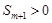 | D.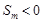 ,且 ,且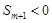 |
设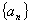 为等差数列,公差
为等差数列,公差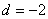 ,
,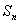 为其前
为其前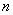 项和,若
项和,若 ,则
,则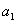 =
=
A. | B. |
C. | D.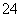 |
数列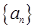 中,
中,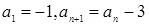 ,则
,则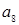 等于( )
等于( )
A.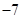 | B. | C.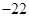 | D.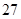 |
等差数列{an}的通项公式为an=2n+1,其前n项的和为Sn,则数列 的前10项的和为( ).
的前10项的和为( ).
| A.120 | B.70 | C.75 | D.100 |
已知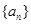 为等差数列,其公差为-2,且a7是a3与a9的等比中项,Sn为
为等差数列,其公差为-2,且a7是a3与a9的等比中项,Sn为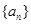 的前n项和(
的前n项和( N*),则S10的值为 ( )
N*),则S10的值为 ( )
| A.-110 | B.-90 | C.90 | D.110 |
等差数列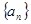 中,若
中,若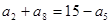 ,则
,则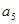 等于( )
等于( )
| A.3 | B.4 | C.5 | D.6 |
 有两个不同的零点
有两个不同的零点 ,且方程
,且方程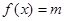 有两个不同的实根
有两个不同的实根 .若把这四个数按从小到大排列构成等差数列,则实数
.若把这四个数按从小到大排列构成等差数列,则实数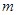 的值为
的值为