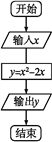
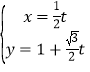题目内容
【题目】设函数![]() .若曲线
.若曲线![]() 在点
在点![]() 处的切线方程为
处的切线方程为
![]() (
(![]() 为自然对数的底数).
为自然对数的底数).
(1)求函数![]() 的单调区间;
的单调区间;
(2)若关于![]() 的不等式
的不等式![]() 在
在![]() 上恒成立,求实数
上恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1) 函数![]() 的单调递减区间是
的单调递减区间是![]() ,单调递增区间是
,单调递增区间是![]()
(2) ![]()
【解析】试题分析:(1)第(1)问,先根据曲线![]() 在点
在点![]() 处的切线方程为
处的切线方程为
![]() 求出m=1,n=0,再利用导数求函数f(x)的单调区间.(2)第(2)问,先把原命题转化为函数
求出m=1,n=0,再利用导数求函数f(x)的单调区间.(2)第(2)问,先把原命题转化为函数![]() 对任意
对任意![]() 恒成立,再利用导数求函数H(x)的单调性,检验每一种情况下H(x)的最大值是否小于零.
恒成立,再利用导数求函数H(x)的单调性,检验每一种情况下H(x)的最大值是否小于零.
试题解析:
(1)函数![]() 定义域为
定义域为![]() .
.![]() 得
得![]() ,
,
![]() ,即
,即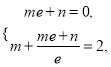 所以
所以![]() .所以
.所以![]() ,
,
![]() .函数
.函数![]() 的单调递减区间是
的单调递减区间是![]() ,单调递增区间是
,单调递增区间是![]() .
.
(2)由题得函数![]() 对任意
对任意![]() 恒成立,
恒成立,
即不等式![]() 对任意
对任意![]() 恒成立.
恒成立.
又![]() ,当
,当![]() 即
即![]() 恒成立时,
恒成立时,
函数![]() 递减,设
递减,设![]() ,则
,则![]() ,所以
,所以![]() ,即
,即![]() ,符合题意;
,符合题意;
当![]() 时,
时, ![]() 恒成立,此时函数
恒成立,此时函数![]() 单调递增.于是不等式
单调递增.于是不等式![]() 对任意
对任意![]() 恒成立,不符合题意;
恒成立,不符合题意;
当![]() 时,设
时,设![]() ,
,
则![]()
![]() ;
;
当![]() 时,
时, ![]() ,此时
,此时![]() 单调递增,
单调递增,
![]()
![]() ,
,
故当![]() 时,函数
时,函数![]() 递增.于是当
递增.于是当![]() 时,
时, ![]() 成立,不符合题意;
成立,不符合题意;
综上所述,实数![]() 的取值范围为:
的取值范围为: ![]() .
.
点睛:本题的难点在于得到![]() 后如何解不等式
后如何解不等式![]() >0或
>0或![]() <0,只有解出了不等式才能得到函数H(x)的单调区间.本题利用了再构造再求导的方法(即二次求导).当我们求出函数f(x)的导数
<0,只有解出了不等式才能得到函数H(x)的单调区间.本题利用了再构造再求导的方法(即二次求导).当我们求出函数f(x)的导数![]() 之后,如果
之后,如果![]() 不易解出,可以利用二次求导找不等式的解集,从而找到原函数的单调性.
不易解出,可以利用二次求导找不等式的解集,从而找到原函数的单调性.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目