题目内容
若函数y=f(x)存在反函数y=f-1(x),且函数y=tan
-f(x)的图象过点(2,
-
),则函数y=f-1(x)-(arcsinx+arccosx)的图象一定过点
| πx |
| 6 |
| 3 |
| 1 |
| 3 |
(
,2-
)
| 1 |
| 3 |
| π |
| 2 |
(
,2-
)
.| 1 |
| 3 |
| π |
| 2 |
分析:由函数y=f(x)的反函数为y=f-1(x),且函数y=tan
-f(x)的图象过点(2,
-
),代入计算出函数y=f(x)的图象过哪一个点,根据原函数与反函数图象的关系,我们易得函数y=f(x)的反函数y=f-1(x)过什么点,进而得到函数y=f-1(x)-(arcsinx+arccosx)的图象过的定点.
| πx |
| 6 |
| 3 |
| 1 |
| 3 |
解答:解:∵函数y=tan
-f(x)的图象过点(2,
-
),
∴
-
=tan
-f(2)
即f(2)=
即函数y=f(x)的图象过点(2,
)
则函数y=f(x)的反函数y=f-1(x)过(
,2)点
∴函数y=f-1(x)-(arcsinx+arccosx)的图象一定过点(
,2-
),
故答案为:(
,2-
).
| πx |
| 6 |
| 3 |
| 1 |
| 3 |
∴
| 3 |
| 1 |
| 3 |
| π |
| 3 |
即f(2)=
| 1 |
| 3 |
即函数y=f(x)的图象过点(2,
| 1 |
| 3 |
则函数y=f(x)的反函数y=f-1(x)过(
| 1 |
| 3 |
∴函数y=f-1(x)-(arcsinx+arccosx)的图象一定过点(
| 1 |
| 3 |
| π |
| 2 |
故答案为:(
| 1 |
| 3 |
| π |
| 2 |
点评:本题考查的知识点是函数的图象及图象的变化,处理本题的核心是:互为反函数的两个函数图象关于直线y=x对称,具体为:函数y=f(x)的图象过(a,b)点,则函数y=f(x)存在反函数y=f-1(x)的图象过(b,a)点.

练习册系列答案
相关题目
 的图象和直线y=x无交点,现有下列结论:
的图象和直线y=x无交点,现有下列结论: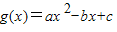 的图象与直线y=-x也一定没有交点.
的图象与直线y=-x也一定没有交点. 的图象和直线y=x无交点,现有下列结论:
的图象和直线y=x无交点,现有下列结论: 的图象与直线y=-x也一定没有交点.
的图象与直线y=-x也一定没有交点. 的图象和直线y=x无交点,现有下列结论:
的图象和直线y=x无交点,现有下列结论: 的图象与直线y=-x也一定没有交点.
的图象与直线y=-x也一定没有交点.