题目内容
在△ABC中，
，D是BC边上任意一点（D与B，C不重合）且
=
- A.
- B.
- C.
- D.
B
分析：作高AE，不妨设E在CD上，设AE=h，CE=x，CD=p，BD=q，则DE=p-x，BE=p+q-x，根据
，可得pq=BD•CD=q（q+2p-2x），从而可得结论．
解答：作高AE，不妨设E在CD上，设AE=h，CE=x，CD=p，BD=q，则DE=p-x，BE=p+q-x，
则AD2=AE2+DE2=h2+（p-x）2，AB2=AE2+BE2=h2+（p+q-x）2，
所以AB2-AD2=（p+q-x）2-（p-x）2=2pq-2xq+q2，
∵，
∴pq=BD•CD=q（q+2p-2x），
∵q≠0，∴p=q+2p-2x，
∴x=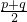
=
，
即E为BC中点，于是ABC为等腰三角形．
∵顶角为
，∴底角B=
故选B．
点评：本题主要考查了解三角形问题．解题的关键是通过题设条件建立数学模型，考查了学生分析问题和解决问题的能力．
分析：作高AE，不妨设E在CD上，设AE=h，CE=x，CD=p，BD=q，则DE=p-x，BE=p+q-x，根据
，可得pq=BD•CD=q（q+2p-2x），从而可得结论．解答：作高AE，不妨设E在CD上，设AE=h，CE=x，CD=p，BD=q，则DE=p-x，BE=p+q-x，
则AD2=AE2+DE2=h2+（p-x）2，AB2=AE2+BE2=h2+（p+q-x）2，
所以AB2-AD2=（p+q-x）2-（p-x）2=2pq-2xq+q2，
∵
，∴pq=BD•CD=q（q+2p-2x），
∵q≠0，∴p=q+2p-2x，
∴x=
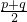=，即E为BC中点，于是ABC为等腰三角形．
∵顶角为
，∴底角B=故选B．
点评：本题主要考查了解三角形问题．解题的关键是通过题设条件建立数学模型，考查了学生分析问题和解决问题的能力．
练习册系列答案
心算口算巧算一课一练系列答案
应用题作业本系列答案
相关题目
在△ABC中，设D是BC边上的一点，且满足
=2
，
=λ
+μ
，则λ+μ的值为（ ）
| CD |
| DB |
| CD |
| AB |
| AC |
A、
| ||
B、
| ||
| C、1 | ||
| D、0 |
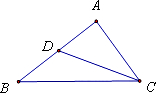如图所示，在△ABC中，点D是边AB的中点，则向量| DC |
A、
| ||||||
B、
| ||||||
C、-
| ||||||
D、-
|
如图，在△ABC中，点D是BC边上靠近B的三等分点，则