题目内容
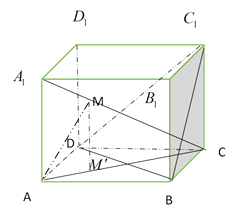
【题目】在棱长为1的正方体![]() 中,点
中,点![]() 关于平面
关于平面![]() 的对称点为
的对称点为![]() ,则
,则![]() 与平面
与平面![]() 所成角的正切值为
所成角的正切值为
A. ![]() B.
B. ![]() C.
C. ![]() D. 2
D. 2
【答案】B
【解析】
利用等体积法求得点![]() 到平面
到平面![]() 的距离为
的距离为![]() ,连接
,连接![]() ,连接
,连接![]() ,可证
,可证![]() 平面
平面![]() ,由于点
,由于点![]() 关于平面
关于平面![]() 的对称点为
的对称点为![]() ,则点
,则点![]() 在线段
在线段![]() 上,根据线段的比例关系可得
上,根据线段的比例关系可得![]() ,从而找出点
,从而找出点![]() 的位置,过
的位置,过![]() 作
作![]() 的垂线交
的垂线交![]() 于
于![]() ,从而可得
,从而可得![]() 平面
平面![]() ,所以
,所以![]() 与平面
与平面![]() 所成角为
所成角为![]() ,求出其正切值即可得到答案。
,求出其正切值即可得到答案。
由题可得![]() ,
,
由于![]() ,即
,即![]() ,则
,则![]() ,解得:
,解得:![]() ,所以点
,所以点![]() 到平面
到平面![]() 的距离为
的距离为![]() ,
,
连接![]() ,连接
,连接![]() ,由于在正方体
,由于在正方体![]() 中,
中,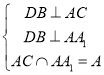 ,则
,则![]() 平面
平面![]() ,所以
,所以![]() ,同理可证:
,同理可证:![]() 平面
平面![]() ,得到:
,得到:![]() ,
,
则可得: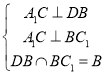 ,故
,故![]() 平面
平面![]()
由于点![]() 关于平面
关于平面![]() 的对称点为
的对称点为![]() ,则点
,则点![]() 在线段
在线段![]() 上,
上,
因为点![]() 到平面
到平面![]() 的距离为
的距离为![]() ,则
,则![]() ,
,
在正方体![]() 中,
中,![]() ,故
,故![]() ,
,
所以点![]() 为
为![]() 的三等分点,过
的三等分点,过![]() 作
作![]() 的垂线交
的垂线交![]() 于
于![]() ,
,
则![]() ,
,![]() ,
,![]()
由于![]() 平面
平面![]() ,则
,则![]() 平面
平面![]() ,
,
连接![]() ,则
,则![]() 与平面
与平面![]() 所成角为
所成角为![]() ,
,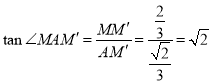
所以![]() 与平面
与平面![]() 所成角的正切值为:
所成角的正切值为:![]()
故答案选B

练习册系列答案
相关题目