题目内容

f（x）=1+（1+x）+（1+x）²+（1+x）³+…+（1+x）ⁿ，则f'（0）等于

A.
n
B.
n-1
C.
n!
D.
$数学公式$ n（n+1）

D
分析：先整理为关于x的n次多项式，进而求导即可求出．
解答：令 $\text{[math]}$ $\text{[math]}$ ，
∴ $\text{[math]}$ ，
∴f'（0）=a₁，又a₁=1+2+3+…+n= $\text{[math]}$ n（n+1），
∴ $\text{[math]}$ ．
故选D．
点评：熟练化简和求导是解题的关键．

练习册系列答案

典元教辅冲刺金牌小升初押题卷系列答案

金考卷中考试题汇编45套系列答案

鸿鹄志文化期末冲刺王暑假作业系列答案

中考模拟预测卷系列答案

小学拓展课堂突破系列答案

字词句段篇章语言训练系列答案

口算应用题整合集训系列答案

小学升初中教材学法指导系列答案

小学生奥数训练营系列答案

中考红8套系列答案

相关题目

设函数f（x）=a²x²（a＞0），g（x）=blnx．
（1）若函数y=f（x）图象上的点到直线x-y-3=0距离的最小值为

，求a的值；
（2）关于x的不等式（x-1）²＞f（x）的解集中的整数恰有3个，求实数a的取值范围；
（3）对于函数f（x）与g（x）定义域上的任意实数x，若存在常数k，m，使得f（x）≥kx+m和g（x）≤kx+m都成立，则称直线y=kx+m为函数f（x）与g（x）的“分界线”．设a=

，b=e，试探究f（x）与g（x）是否存在“分界线”？若存在，求出“分界线”的方程；若不存在，请说明理由．

（2013•黄埔区一模）对于函数y=f（x）与常数a，b，若f（2x）=af（x）+b恒成立，则称（a，b）为函数f（x）的一个“P数对”；若f（2x）≥af（x）+b恒成立，则称（a，b）为函数f（x）的一个“类P数对”．设函数f（x）的定义域为R⁺，且f（1）=3．
（1）若（1，1）是f（x）的一个“P数对”，求f（2ⁿ）（n∈N*）；
（2）若（-2，0）是f（x）的一个“P数对”，且当x∈[1，2）时f（x）=k-|2x-3|，求f（x）在区间[1，2ⁿ）（n∈N*）上的最大值与最小值；
（3）若f（x）是增函数，且（2，-2）是f（x）的一个“类P数对”，试比较下列各组中两个式子的大小，并说明理由．
①f（2^-n）与2^-n+2（n∈N*）；
②f（x）与2x+2（x∈（0，1]）．

设函数f（x）=a²x²（a＞0），g（x）=blnx．
（1）若函数y=f（x）图象上的点到直线x-y-3=0距离的最小值为2

，求a的值；
（2）关于x的不等式（x-1）²＞f（x）的解集中的整数恰有3个，求实数a的取值范围；
（3）对于函数f（x）与g（x）定义域上的任意实数x，若存在常数k，m，使得f（x）≥kx+m和g（x）≤kx+m都成立，则称直线y=kx+m为函数f（x）与g（x）的“分界线”．设a=

，b=e，试探究f（x）与g（x）是否存在“分界线”？若存在，求出“分界线”的方程；若不存在，请说明理由．

对于函数y=f（x）与常数a，b，若f（2x）=af（x）+b恒成立，则称（a，b）为函数f（x）的一个“P数对”；若f（2x）≥af（x）+b恒成立，则称（a，b）为函数f（x）的一个“类P数对”．设函数f（x）的定义域为R⁺，且f（1）=3．
（1）若（1，1）是f（x）的一个“P数对”，求f（2ⁿ）（n∈N*）；
（2）若（-2，0）是f（x）的一个“P数对”，且当x∈[1，2）时f（x）=k-|2x-3|，求f（x）在区间[1，2ⁿ）（n∈N*）上的最大值与最小值；
（3）若f（x）是增函数，且（2，-2）是f（x）的一个“类P数对”，试比较下列各组中两个式子的大小，并说明理由．
①f（2^-n）与2^-n+2（n∈N*）；
②f（x）与2x+2（x∈（0，1]）．

下面对命题“函数f（x）=x+

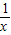是奇函数”的证明不是综合法的是（）
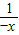A．?x∈R且x≠0有f（-x）=（-x）+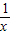

）=-f（x），∴f（x）是奇函数
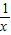B．?x∈R且x≠0有f（x）+f（-x）=x+

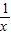）=0，∴f（x）=-f（-x），∴f（x）是奇函数
C．?x∈R且x≠0，∵f（x）≠0，∴

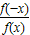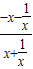=-1，∴f（-x）=-f（x），∴f（x）是奇函数
D．取x=-1，f（-1）=-1+

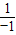=-2，又f（1）=1+

=2