题目内容
某工厂在甲、乙两地的两个分厂各生产某种机器12台和6台,现销售给 地10台,
地10台, 地8台.已知从甲地调动1台至
地8台.已知从甲地调动1台至 地,
地, 地的运费分别为400元和800元,从乙地调运1台至
地的运费分别为400元和800元,从乙地调运1台至 地,
地, 地的费用分别为300元和500元.
地的费用分别为300元和500元.
(1) 设从乙地调运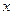 台至
台至 地,求总费用
地,求总费用 关于台数
关于台数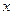 的函数解析式;
的函数解析式;
(2) 若总运费不超过9000元,问共有几种调运方案;
(3) 求出总运费最低的调运方案及最低的费用.
 地10台,
地10台, 地8台.已知从甲地调动1台至
地8台.已知从甲地调动1台至 地,
地, 地的运费分别为400元和800元,从乙地调运1台至
地的运费分别为400元和800元,从乙地调运1台至 地,
地, 地的费用分别为300元和500元.
地的费用分别为300元和500元.(1) 设从乙地调运
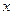 台至
台至 地,求总费用
地,求总费用 关于台数
关于台数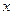 的函数解析式;
的函数解析式;(2) 若总运费不超过9000元,问共有几种调运方案;
(3) 求出总运费最低的调运方案及最低的费用.
(1) (2)共有三种调运方案
(2)共有三种调运方案
(3)当 时,总运费
时,总运费 最低,
最低, (元)
(元)
 (2)共有三种调运方案
(2)共有三种调运方案(3)当
 时,总运费
时,总运费 最低,
最低, (元)
(元)由甲、乙两地调运至 ,
, 两地的机器台数及费用(元)如下表.
两地的机器台数及费用(元)如下表.
(1)依题意得
 ,
,
即 .
.
(2)由 ,解得
,解得 .
.
因为 ,
, ,所以
,所以 ,1,2.
,1,2.
答:共有三种调运方案.
(3)由一次函数的单调性知,当 时,总运费
时,总运费 最低,
最低, (元).
(元).
答:从乙地调6台给 地,甲地调10台给
地,甲地调10台给 地,调2台给
地,调2台给 地的调动方案的总运费最低,最低运费为8600元.
地的调动方案的总运费最低,最低运费为8600元.
 ,
, 两地的机器台数及费用(元)如下表.
两地的机器台数及费用(元)如下表.| 调出地 | 甲地 |  乙地 乙地 | ||
| 调至地 |  地 地 |  地 地 |  地 地 |  地 地 |
| 台数 |  |  | 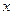 |  |
| 每台运费 | 400 | 800 | 300 | 500 |
| 运费合计 | | |  | |
| |  |  | |  |
 ,
,即
 .
.(2)由
 ,解得
,解得 .
.因为
 ,
, ,所以
,所以 ,1,2.
,1,2.答:共有三种调运方案.
(3)由一次函数的单调性知,当
 时,总运费
时,总运费 最低,
最低, (元).
(元).答:从乙地调6台给
 地,甲地调10台给
地,甲地调10台给 地,调2台给
地,调2台给 地的调动方案的总运费最低,最低运费为8600元.
地的调动方案的总运费最低,最低运费为8600元.
练习册系列答案
相关题目
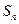 为数列
为数列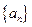 的前
的前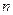 项和,且
项和,且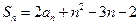 ,
,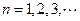 ,(Ⅰ)求证:数列
,(Ⅰ)求证:数列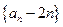 为等比数列;(Ⅱ)设
为等比数列;(Ⅱ)设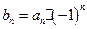 ,求数列
,求数列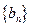 的前
的前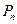 ;(Ⅲ)设
;(Ⅲ)设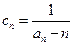 ,数列
,数列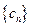 的前
的前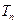 ,求证:
,求证: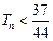 .
. 的图象上任意两点,且
的图象上任意两点,且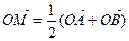 ,已知点M的横坐标为
,已知点M的横坐标为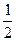 .
.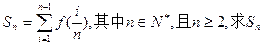 ;
;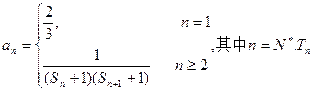 为数列
为数列 的前n项和,若
的前n项和,若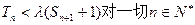 都成立,试求
都成立,试求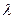 的取值范围.
的取值范围.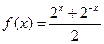
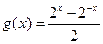
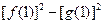 ;
;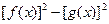 是定值
是定值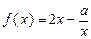
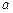
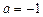 时,求函数
时,求函数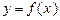 的值域;
的值域;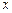 的值
的值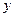 (单位:万元)随销售利润
(单位:万元)随销售利润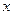 (单位:万元)的增加而增加,但奖金总数不超过
(单位:万元)的增加而增加,但奖金总数不超过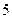 万元,同时奖金不超过利润的
万元,同时奖金不超过利润的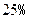 .现有三个奖励模型:
.现有三个奖励模型: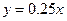 ,
,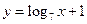 ,
,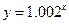 .其中哪个模型能符合公司的要求?
.其中哪个模型能符合公司的要求?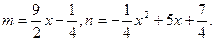

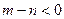
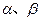 是方程
是方程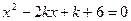 的两个实根,则
的两个实根,则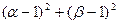 的最小值是多少?
的最小值是多少? ,且
,且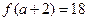 ,
,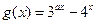 的定义域为[-1,1]。
的定义域为[-1,1]。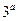 值及函数
值及函数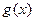 的解析式;
的解析式;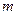 有解,求实数
有解,求实数