题目内容
(本小题满分12分)设直线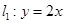 与直线
与直线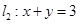 交于
交于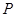 点.
点.
(1)当直线 过
过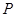 点,且与直线
点,且与直线 垂直时,求直线
垂直时,求直线 的方程;
的方程;
(2)当直线 过
过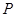 点,且坐标原点
点,且坐标原点 到直线
到直线 的距离为
的距离为 时,求直线
时,求直线 的方程.
的方程.
(1) 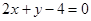 . (2)
. (2) 或
或 .
.
解析试题分析:由 ,解得点
,解得点 . ………………………2分
. ………………………2分
(1)因为 ⊥
⊥ ,所以直线
,所以直线 的斜率
的斜率 , ………………………4分
, ………………………4分
又直线 过点
过点 ,故直线
,故直线 的方程为:
的方程为: ,即
,即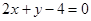 . …………………………6分
. …………………………6分
(2)因为直线 过点
过点 ,当直线
,当直线 的斜率存在时,可设直线
的斜率存在时,可设直线 的方程为
的方程为 即
即 . …………………7分
. …………………7分
所以坐标原点 到直线
到直线 的距离
的距离 ,解得
,解得 , …………9分
, …………9分
因此直线 的方程为:
的方程为: ,即
,即 . …………10分
. …………10分
当直线 的斜率不存在时,直线
的斜率不存在时,直线 的方程为
的方程为 ,验证可知符合题意.[来
,验证可知符合题意.[来
综上所述,所求直线 的方程为
的方程为 或
或 . ………………12分
. ………………12分
考点:本题主要考查直线与直线的位置关系,求直线方程。
点评:典型题,在直线与直线的位置关系问题中,平行、垂直是两类常见题型,如果利用斜率关系加以研究,必须考虑直线斜率不存在的可能情况。(2)是易错题。

练习册系列答案
 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
 交于不同的两点A,B;O为坐标原点。
交于不同的两点A,B;O为坐标原点。 ,试探究在曲线C上仅存在几个点到直线L的距离恰为
,试探究在曲线C上仅存在几个点到直线L的距离恰为 ?并说明理由;
?并说明理由;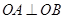 ,且a>b,
,且a>b, ,试求曲线C的离心率e的取值范围。
,试求曲线C的离心率e的取值范围。 所围成的封闭图形的面积为
所围成的封闭图形的面积为 ,曲线
,曲线 的内切圆半径为
的内切圆半径为 .记
.记 为以曲线
为以曲线 是过椭圆
是过椭圆 是线段
是线段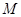 是
是 (
( 为坐标原点),当点
为坐标原点),当点 在椭圆
在椭圆 的面积的最小值.
的面积的最小值. 中,F1、F2分别为其左右焦点,点P在双曲线上运动,求△PF1F2的重心G的轨迹方程.
中,F1、F2分别为其左右焦点,点P在双曲线上运动,求△PF1F2的重心G的轨迹方程. ,它的离心率为
,它的离心率为 ,一个焦点和抛物线
,一个焦点和抛物线 的焦点重合,过直线
的焦点重合,过直线 上一点M引椭圆
上一点M引椭圆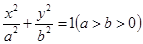 上的点
上的点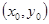 处的椭圆的切线方程是
处的椭圆的切线方程是 . 求证:直线
. 求证:直线 恒过定点
恒过定点 ;并出求定点
;并出求定点 ,使得
,使得 恒成立?(点
恒成立?(点 被双曲线
被双曲线 截得的弦长;
截得的弦长; 的直线被双曲线
的直线被双曲线 的焦点F,与抛物线交于两点A,B,
的焦点F,与抛物线交于两点A,B,
 的方程;
的方程; 的面积S的最大值;
的面积S的最大值; .
. :y=kx+m(m≠0)与(Ⅰ)中的轨迹C交于不同的两点A,B.
:y=kx+m(m≠0)与(Ⅰ)中的轨迹C交于不同的两点A,B. 的中心为
的中心为 ,长轴的两个端点为
,长轴的两个端点为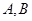 ,右焦点为
,右焦点为 ,
, .若椭圆
.若椭圆 ,
, 上的射影为
上的射影为 的面积为5.
的面积为5. =1,直线
=1,直线 =1,试证明:当点
=1,试证明:当点 在椭圆
在椭圆 与圆
与圆