题目内容
(本小题满分12分)
(1)求直线 被双曲线
被双曲线 截得的弦长;
截得的弦长;
(2)求过定点 的直线被双曲线
的直线被双曲线 截得的弦中点轨迹方程。
截得的弦中点轨迹方程。
(1)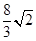 (2)
(2)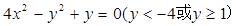
解析试题分析:由
 得
得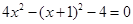 得
得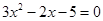 (*)
(*)
设方程(*)的解为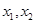 ,则有
,则有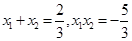 得,
得,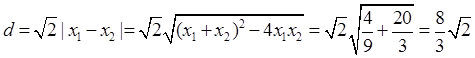 ……6分
……6分
(2)方法一:若该直线的斜率不存在时与双曲线无交点,则设直线的方程为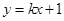 ,它被双曲线截得的弦为
,它被双曲线截得的弦为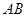 对应的中点为
对应的中点为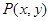 ,
,
由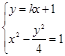 得
得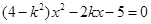 (*)
(*)
设方程(*)的解为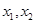 ,则
,则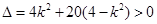 ,
,
∴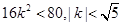 ,
,
且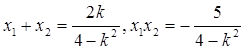 ,
,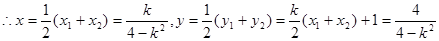 ,
,
得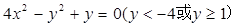 。……12分
。……12分
方法二:设弦的两个端点坐标为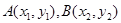 ,弦中点为
,弦中点为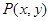 ,则
,则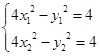 得:
得: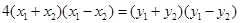 ,
,
∴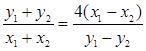 , 即
, 即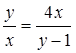 ,
,
即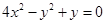 (图象的一部分) ……12分
(图象的一部分) ……12分
考点:直线与圆锥曲线相交的弦长及求动点的轨迹方程
点评:用到的弦长公式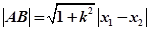 ,本题求动点的轨迹方程用到的是参数法和点差法,其中关于弦中点的问题点差法是常采用的方法
,本题求动点的轨迹方程用到的是参数法和点差法,其中关于弦中点的问题点差法是常采用的方法

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
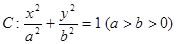 过点
过点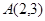 ,且离心率
,且离心率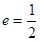 .
.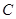 的标准方程;
的标准方程;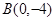 的直线
的直线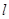 交椭圆于不同的两点M、N,且满足
交椭圆于不同的两点M、N,且满足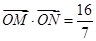 (其中点O为坐标原点),若存在,求出直线
(其中点O为坐标原点),若存在,求出直线 作直线
作直线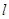 与抛物线
与抛物线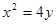 相交于两点
相交于两点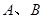 ,圆
,圆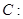
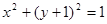
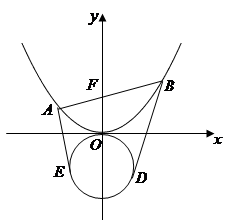
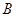 处的切线恰好与圆
处的切线恰好与圆 相切,求直线
相切,求直线 ,
,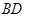 试求
试求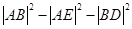 的取值范围.
的取值范围.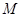 经过定点
经过定点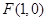 ,且与直线
,且与直线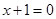 相切。
相切。 方程;
方程;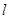 过定点
过定点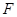 与曲线
与曲线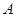 、
、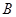 两点:
两点: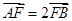 ,求直线
,求直线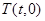 始终在以
始终在以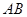 为直径的圆内,求
为直径的圆内,求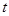 的取值范围。
的取值范围。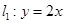 与直线
与直线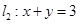 交于
交于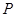 点.
点. 过
过 垂直时,求直线
垂直时,求直线 到直线
到直线 时,求直线
时,求直线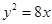 的焦点,M的离心率
的焦点,M的离心率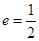 ,过M的右焦点F作不与坐标轴垂直的直线
,过M的右焦点F作不与坐标轴垂直的直线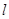 ,交M于A,B两点。
,交M于A,B两点。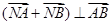 ,求实数t的取值范围。
,求实数t的取值范围。 ,并经过点
,并经过点 ,求此双曲线的标准方程.
,求此双曲线的标准方程. 的双曲线的方程.
的双曲线的方程. 的最小值为 .
的最小值为 . 在曲线
在曲线 上,点
上,点 在曲线
在曲线 上,点
上,点 在曲线
在曲线 上,则
上,则 的最大值是 .
的最大值是 .