题目内容
(08年山西大学附中五模理) 已知椭圆![]() 两焦点分别为
两焦点分别为![]() 、
、![]() ,
,![]() 是椭圆在第一象限弧上一点,并满
是椭圆在第一象限弧上一点,并满
足![]() ,过
,过![]() 作倾斜角互补的两条直线
作倾斜角互补的两条直线![]() 、
、![]() 分别交椭圆于
分别交椭圆于![]() 、
、![]() 两点.
两点.
(Ⅰ)求![]() 点坐标; (Ⅱ)求证直线
点坐标; (Ⅱ)求证直线![]() 的斜率为定值;
的斜率为定值;
(Ⅲ)求![]() 面积的最大值.
面积的最大值.
解析:(Ⅰ)由题可得![]() ,
,![]() ,设
,设![]()
则![]() ,
,![]() ,
,
∴![]() ,∵点
,∵点![]() 在曲线上,则
在曲线上,则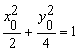 ,∴
,∴![]() ,从而
,从而![]() ,得
,得![]() .则点P的坐标为
.则点P的坐标为![]() .
.
(Ⅱ)由题意知,两直线PA、PB的斜率必存在,设PB的斜率为![]() ,
,
则BP的直线方程为:![]() .由
.由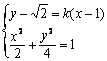 得
得![]()
![]() ,设
,设![]() ,则
,则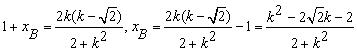 ,
,
同理可得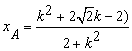 ,则
,则![]() ,
,![]() .
.
所以:AB的斜率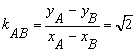 为定值.
为定值.
(Ⅲ)设AB的直线方程:![]() .
.
由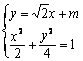 ,得
,得![]() ,
,
由![]() ,得
,得![]()
P到AB的距离为![]() ,
,
则![]()
![]() .
.
当且仅当![]() 取等号
取等号
∴三角形PAB面积的最大值为![]() 。
。


练习册系列答案
相关题目