题目内容
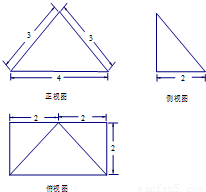已知四棱锥P-ABCD的三视图如图所示，则四棱锥P-ABCD的四个侧面中面积最大的是（ ）A．6
B．8
C．
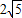
D．3
【答案】分析：三视图复原的几何体是四棱锥，利用三视图的数据直接求解四棱锥P-ABCD的四个侧面中面积，得到最大值即可．
解答：解：因为三视图复原的几何体是四棱锥，顶点在底面的射影是底面矩形的长边的中点，底面边长分别为4，2，
后面是等腰三角形，腰为3，所以后面的三角形的高为：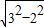
=
，
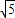所以后面三角形的面积为：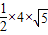
=2
．
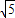两个侧面面积为：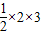
=3，前面三角形的面积为：
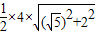=6，
四棱锥P-ABCD的四个侧面中面积最大的是前面三角形的面积：6．
故选A．
点评：本题考查三视图与几何体的关系，几何体的侧面积的求法，考查计算能力．
解答：解：因为三视图复原的几何体是四棱锥，顶点在底面的射影是底面矩形的长边的中点，底面边长分别为4，2，
后面是等腰三角形，腰为3，所以后面的三角形的高为：
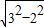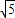=，所以后面三角形的面积为：
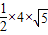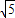=2．两个侧面面积为：
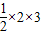=3，前面三角形的面积为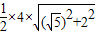：=6，四棱锥P-ABCD的四个侧面中面积最大的是前面三角形的面积：6．
故选A．
点评：本题考查三视图与几何体的关系，几何体的侧面积的求法，考查计算能力．
练习册系列答案
相关题目
如图，已知四棱锥P--ABC的底面ABCD为正方形，PA⊥平面ABCD，PA=AB=2，e为PC的中点，F为AD的中点．
如图，已知四棱锥P-ABCD的底面是直角梯形，∠ABC=∠BCD=90°，AB=BC=2CD=2，PB=PC，侧面PBC⊥底面ABCD，O是BC的中点．
已知四棱锥P-ABCD的底面是直角梯形，∠ABC=∠BCD=90°，E为BC中点，AE与BD交于O点，AB=BC=2CD=2，BD⊥PE．
如图，已知四棱锥P-ABCD中，PA⊥平面ABCD，底面ABCD是直角梯形，∠DAB=∠ABC=90°，E是线段PC上一点，PC⊥平面BDE．