题目内容
若|loga |=loga
|=loga ,|logba|=-logba,则a,b满足的条件是( )
,|logba|=-logba,则a,b满足的条件是( )
 |=loga
|=loga ,|logba|=-logba,则a,b满足的条件是( )
,|logba|=-logba,则a,b满足的条件是( )| A.a>1,b>1 | B.0<a<1,b>1 |
| C.a>1,0<b<1 | D.0<a<1,0<b<1 |
B
先利用|m|=m,则m≥0,|m|=-m,则m≤0,将条件进行化简,然后利用对数函数的单调性即可求出a和b的范围.
∵|loga |=loga
|=loga ,
,
∴loga ≥0=loga1,根据对数函数的单调性可知0<a<1.
≥0=loga1,根据对数函数的单调性可知0<a<1.
∵|logba|=-logba,
∴logba≤0=logb1,但b≠1,所以根据对数函数的单调性可知b>1.
∵|loga
 |=loga
|=loga ,
,∴loga
 ≥0=loga1,根据对数函数的单调性可知0<a<1.
≥0=loga1,根据对数函数的单调性可知0<a<1.∵|logba|=-logba,
∴logba≤0=logb1,但b≠1,所以根据对数函数的单调性可知b>1.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
 ,则a=________;
,则a=________; 是奇函数,则使f(x)<0的x的取值范围是________;
是奇函数,则使f(x)<0的x的取值范围是________;
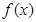 为奇函数,当
为奇函数,当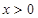 时,
时,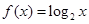 ,则满足不等式
,则满足不等式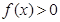 的
的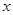 的取值范围是 .
的取值范围是 .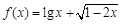 的定义域为
的定义域为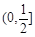
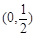
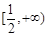
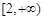
 中,
中, ,则
,则 的值是( )
的值是( )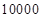


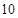
 的图像过点
的图像过点 ,则
,则 ________.
________.